First, we must fully understand the explanation of a very common phenomenon of our everyday experience; or rather, of a large number of related phenomena. The phenomena I’m talking about are things like these:
|
|
In general, things seem to deteriorate if left to their own devices. Because of this deterioration, we observe an asymmetry between the “before” and the “after”. For example, the smoke was contained within a small volume before, and has expanded into a larger volume after. And because of this asymmetry of processes in the macro-world we can always tell which direction of time to label “past”, and which “future”.
But physicists have long observed that there is nothing in the laws of physics, as known since Galileo’s time, that points to some kind of asymmetry between the “before now” and the “after now”. Laws of physics are symmetric(*) with respect to time. For instance, let’s look at what Brian Greene writes in The Fabric of the Cosmos:[1]
“It turns out that the known and accepted laws of physics show no [temporal] asymmetry […]: each direction in time, forward and backward, is treated by the laws without distinction. And that’s the origin of a huge puzzle. Nothing in the equations of fundamental physics shows any sign of treating one direction in time differently from the other, and that is totally at odds with everything we experience.” (p. 13, emphasis in the original.)
Want to see temporal symmetry in action? Then
watch the following figure (assume the moving circles are
molecules of a substance jostling and bumping against some other,
invisible molecules, thus performing random walks). Click
on
![]() to
start.
to
start.
|
|
Figure 1.2: “Molecules”
moving randomly. Click on
![]() to
start.
to
start.
When we look at a microworld “movie” from up close (or a movie showing some object that moves according to Newton’s laws of motion), we can’t tell whether the movie is running forward or backward in time. For example, in the above figure, we don’t know whether I set the movie running forward, or in reverse. The symmetric treatment of the two temporal directions (past and future) in Newton’s laws of motion implies that whether time runs forward, or backwards, the laws will predict exactly the same outcome. But why are physicists puzzled?
I think what puzzles physicists like Greene is this: on one hand, they know that we, human beings, have some way of distinguishing between past and future by using our brains. On the other hand, they assume the brain is a physical device, abiding by the laws of physics. So they reason that there should be something in the laws of physics that hints at how a physical device, the brain, manages to distinguish between past and future. But there isn’t!(*) No physical law distinguishes between “before now” and “after now”, so that we could say, “Aha! Perhaps the human (or animal) brain uses this law, so that’s how it makes the distinction!” Isn’t this puzzling? Do we have to conclude that the brain is not strictly a physical device? Does the brain employ some non-physical, immaterial “magic” by which it perceives the asymmetry between past and future?
No, we don’t have to resort to such hocus-pocus. We should refrain from invoking a greater mystery (“immaterial powers”, “magic”) in order to answer a lesser one. The brain can indeed be considered a purely physical device, but what it manages to do is not necessarily describable by the discipline of physics; that is, physics is insufficient to describe the brain. What is required to explain the brain’s perceived properties of time is cognitive science; also, a tad of biology won’t hurt, to explain how brains evolved to acquire such abilities. That’s what this article is about.
But we need to consider things in order. First, we must understand why processes appear temporally asymmetric in the macro-world, because that’s where the long history of time starts.
1.1 The Second Law of Thermodynamics, and What Causes it
The law that causes the deterioration of structures in our familiar macro-world is known as the Second Law of Thermodynamics (2ndLoT) and, contrary to what its name suggests, it’s not a law of physics — strictly speaking — but a law of statistics and geometry. The 2ndLoT states, roughly, the following:
| Physical
systems tend to evolve toward states of greater disorder (or of “higher entropy” in physics jargon). |
The following figure is an example of the
2ndLoT in action. It shows a number of particles arranged in an
orderly fashion, which start moving randomly in space (they
perform “random walks”) as soon as you press on
![]() .
.
|
|
Figure 1.3:
Particles dispersing in space, due to the 2ndLoT. To increase the speed,
click on
![]() repeatedly.
repeatedly.
Think of the particles as the pebbles and gravel that, once upon a time, made up the church of Fig. 1.1. As you can see, although they start at an initially ordered arrangement, they end up dispersed randomly and evenly in space, although there’s nothing in Fig. 1.3 that orders them to disperse away from the center. The particles merely move randomly in space, and will not return to the center “till cows come home”! (And, by the way, now you know why cows don’t ever come back home all by themselves.) The reason for this behavior will be explained in a minute. But first, please note the following.
|
There has been a lot of confusion about what the 2ndLoT really is, even among some scientists. Because it was first observed in the context of thermodynamics (whence its name), some professors of physics or chemistry might claim that what is depicted in Fig. 1.3 is not an illustration of the 2ndLoT. What they miss is that the notion “Second Law of Thermodynamics” is something deeper than what they observe in the context of thermodynamics, in which what disperses is energy (i.e., photons). But the deeper law concerns also the dispersal of mass, like the simulated particles of Fig. 1.3. I discuss this confusion in detail in this page. The law should be known by a more general name — perhaps something like “the Law of Dispersal” — but thermodynamics is its historic origin, so the name stuck with us. |
Now, what causes the 2ndLoT? What kind of “force” is it that “orders” particles to disperse from their original location? It is actually quite easy to see why a particle, on average, will distance itself from its original location. (“On average” means that a single particle in a single observation might be seen to return to its original location at some time, but if we average out a large number of observations — of “walks” of the particle — then the average position of the particle will increase from the origin as time goes by.) Consider the following figure:
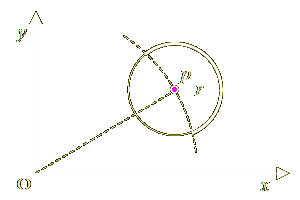
Figure 1.4: Geometric justification of the 2ndLoT
Suppose the particle shown with the purple dot started off at location O, is now at location p, and is “contemplating” to jump to a new location on the xy-plane at a distance r from its present one at p. Therefore, it will end up anywhere on a circle centered at p, having a radius of r (the full circle shown in the figure). Now, of all these “next locations” on that circle, which ones are closer to the origin O, and which ones are farther? The ones that are farther belong to the arc of the circle that is marked in bold, whereas the ones that are closer to O are on the thinner arc. Clearly, the bold arc is slightly longer than the thinner one. This means that particle p has a slightly greater probability to end up on the bold arc (farther with respect to the origin) than on the thinner arc (closer with respect to the origin). This is the reason why, according to probabilities and simple geometry, the particle will find itself at a greater distance from its original location, on average. A mathematical derivation of the speed by which the particle will distance itself from O is given in the previously referenced page (at this point), where it is proven that the speed is proportional to the square root of t, where t is the elapsed time. That’s exactly the formula computed by Einstein in his 1906 paper on Brownian motion.[2]
So we see that the asymmetry of processes in the macro-world is a consequence of the 2ndLoT, which in turn is a consequence of statistics (or probabilities) and simple geometry. Thus, if there are particles in a universe, and these particles extend along the dimension of time,(*) then there will be macroworld temporal asymmetry in that universe. This is a mathematical conclusion, as certain as the Pythagorean theorem, or the statement that 1 + 1 = 2.
Can mathematical results cause the emergence of structures in the macro-world, independently of the known laws of physics, as the latter appear in textbooks of physics? But of course! Consider the situation in the following figure:
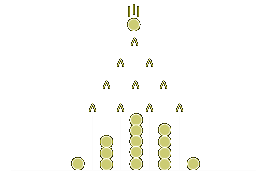
Figure 1.5: Shape formed due to statistics only
Here, balls drop from the top of Fig. 1.5, and upon meeting one of the Λ-shaped obstacles they fall randomly either left or right, with equal probability. The result is the bell-shaped (Gaussian-like) curve formed at the bottom. This is a real-world object, and its shape cannot be predicted by the laws of physics, but only by the laws of probabilities. (Unless, of course, we extend the notion “laws of physics” to include all of known mathematics.)
|
Caveat emptor: the 2ndLoT, although it explains the macro-world temporal asymmetry, does not explain the overall temporal “asymmetry of the universe”, i.e., the fact that the universe started small at the Big Bang and continues growing in size for billions of years. The universal temporal asymmetry requires some other, extra-physical (cosmological) explanation. The fact that the asymmetry of the universe is unrelated to the 2ndLoT becomes clear if we consider a hypothetical situation in which the universe is in the process of a “Big Crunch”: in that case, the 2ndLoT would still hold (material structures would still disintegrate), but the 3D-space of the universe as a whole would be in a process of shrinkage, which would eventually force particles to follow not random, but biased walks, being continually restricted in 3D-space; but this would be an “add-on”, a property “on top of ” the 2ndLoT. |
Let’s pause for a moment and ponder over what we have so far: we concluded that the macroworld ought to be asymmetric along time as long as there are particles in it — there is no escape from this conclusion. But an asymmetry is not the same as a direction. Okay, we could say we distinguish past from future because of their asymmetry, because they look different from each other, but why do we feel as if we move from the past toward the future? Couldn’t we feel we move from the future toward the past? Why do events seem to be coming from an unknown future and relegated into a known past? What causes the direction we feel is there? To see the difference between asymmetry and directionality, consider the shape of a cone (next figure):

Figure 1.6: A cone is an asymmetric object, but it lacks a built-in direction
The cone in Fig. 1.6 is asymmetric along a horizontally-running axis, since it’s thin at its tip, and thick at its base, so tip and base are different, we can tell them apart. But the cone has no preferred direction: we may scan it from tip to base, or from base to tip, or we might as well not scan it at all! What is it that causes us to feel that time is scanned in one particular direction throughout our lives? The answer has to do with what memories are, and how they are formed. This is discussed in the next section.
2. Why Do We Feel There Is a Direction in Time?
Hard questions can sometimes be answered by supposing that the opposite of what the question asks is true. In math, too, often a statement of the form “Prove that P is true” is tackled by saying: “Suppose P is false.” Then one proceeds to conclusions assuming the falsity of P, and reaches some logical contradiction, which leads the thinker to conclude that P must be true.
 |
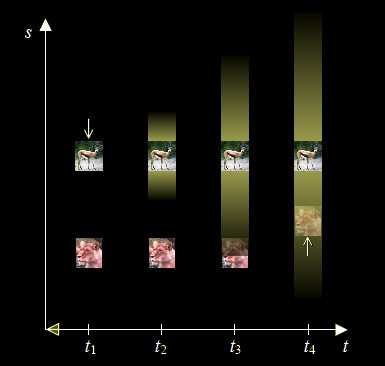
Something analogous will be attempted here. Normally, we perceive a direction in time that goes from order to disorder according to the 2ndLoT, and the question is: “Why do we feel there is that particular direction and not the opposite, or the absence of any direction?” Well, then suppose we don’t perceive the familiar direction in time. What are the consequences of that? That’s how our discussion will develop. But before we can think of abandoning the familiar direction of time, we better think first of a situation with the familiar direction (so we can later reverse it). An all-too-common incident from the world of nature between a gazelle (left) and a lion (right)will help us do just that. |
 |
Suppose that an unsuspecting gazelle is wandering in a region where a lion is resting, and at time t1 the gazelle comes and stops some 100 yards away from the lion (see diagram in Fig. 2.1), grazing the grass, completely unaware of the danger. At first, the lion is also unaware of the gazelle’s presence. However, the smell of the gazelle starts spreading in the environment (time t2), and at some point it reaches the sensitive nose of the lion (time t3). At that time the lion, alerted by the smell, starts moving stealthily toward the source of the smell (time t4). We will let nature decide what will happen from that time on, because what concerns us is what happened up to that time.
Figure 2.1: Successive stages in a natural drama |
What was just described is the normal sequence of events, with time running in the forward direction. Notice that the gazelle is a source of information, because its odor particles disperse in the environment according to the 2ndLoT, inform the lion of the gazelle’s presence, and cause the subsequent event of the lion approaching the gazelle. Now imagine that you see the same “movie”, but running backwards. What would you see? At time t4 you’d see the lion backstepping and moving away from the gazelle. Once at a maximum distance at t3, the lion would stop and “rest” on the ground. At the same time, the odor particles that were in the air and which had been marching miraculously toward the gazelle from all directions, would abandon the vicinity of the lion, whose nose would stop detecting(*) anything interesting. The odor particles would all find their way to their common destination, the gazelle, as if guided by a magic hand. The gazelle would soon depart from the region backstepping, and that would be the end of the story. Or would it? Something doesn’t pan out in this story. Hm... why were those smelly particles directed toward the gazelle? Who, or what force directed them there? |
Naturally we, knowing that the previous story originated from the reversal of the forward-playing movie, realize that the reason the particles ended up at the gazelle is that the movie was played backwards, because “normally” the particles disperse. But now we are trying to see if the backward-running movie could ever be the normal one. We cannot rely on the naturalness of the forward-running movie because our working assumption is: “Suppose we don’t perceive the familiar direction in time; instead, suppose we perceive as normal the opposite direction (the one against the 2ndLoT).”
2.1 The Loss of Causality
So, in a world of time running backward we’d be confronted with the conundrum of the “odor-particle conspiracy”: particles would end up at a common destination, like pilgrims on their way to Mecca. However, real pilgrims have a purpose, plans, and volition that directs them wherever they must go; what do mere particles have that directs them to the same location? That would remain a mystery. But, alas, the world would be full of such mysteries:
-
Molecules of SiO2 (silicon dioxide, or silica) and various other chemicals would gather up from “the four corners of the world” to form first some tiny broken pieces of glass, which would join and keep forming ever larger pieces, until the pieces would, in one final act of pure magic, all gather up seamlessly together and form the single rectangular glass of a now-unbroken window.
-
The brown and yellow leaves of trees would miraculously sort themselves out, each according to its kind, and find their way up into the right kind of tree (never-ever ending up on the wrong type of tree), becoming greener after several days.
-
Speaking of leaves, photons would be emitted from their chloroplasts, and would all eventually be directed toward a nearby star, the Sun, as if photons “knew” which way to go, working against the randomness of the quantum world.
And these magical acts would be only the tip of an iceberg. For you would also see objects act as if they defeated gravity all the time, miraculously jumping with just the right momentum so as to end up at a higher altitude: those would be all the objects that simply fell down from a higher to a lower place in the normal, forward-running movie of the world. For instance, suppose that in “forward time” you hold a stone in your hand, and then you release it, letting it drop to the ground. In “backward time” this stone comes to your hand, but how does it manage to defy gravity? Because an astonishing number of quantum events on the ground conspire to give the stone just the right kind of kick so that it ends up in your palm. So we see that the magic wouldn’t concern just some gazelles and their odor particles; it would be part and parcel of our experience in the everyday world. Indeed, that kind of “magic” would be so prevalent that we wouldn’t be able to explain nature. We feel we have a natural explanation when we say that X happened because of Y. But In our back-running world, most of our “because” statements would be incomplete:
-
We say the plain flooded because there was a lot of rain and the nearby river overflowed. But in the back-running world, the plain was drained. Fine, now why did that happen? What forced copious quantities of water back into the river? Further, what caused the water of the river to form droplets of rain that were kicked skywards forming clouds, “helped” throughout their entire skyward trek by infinitesimal conspiring kicks of air molecules? The “because” is lost; it’s that magical power at work again.
-
Or, consider a landslide in reverse: large quantities of soil would first become wet and muddy, then the mud would be withdrawn, without cause and explanation, collecting on the slope of a nearby hill, perhaps simultaneously revealing houses, livestock, and people — who would magically become alive. Why did that happen? Who knows.
-
Sunken ships would come out of the abyss of the ocean, pushed upward by the water molecules, currents, and small and large eddies in just the right ways, while the sea would become turbulent. The ship would emerge out of the water in the storm, acquiring sailors either through boats or directly from the water. Again, no explanation.
If you’d prefer to watch things instead of imagining about them, then take a look at the following entertaining video:
Figure 2.2: Which song is this?
In the first half of the above video, a guy does various things that are understood normally with time running forward, while he sings a known tune backwards. In the second half, the same video is played backwards. Most likely, the guy produced this video to show to his audience that he can sing backwards. But of particular interest to us are the various time-reversed events in the second half of the video. Watch them, and try to see how many of them start completely unpredictably, and proceed utterly mysteriously, ending up in structures or in situations for which there is no rationale, no way to claim that “X happened because of Y”.
Those examples show that the backward-running world would be inexplicable, which means, causality as we understand it would be gone. Instead, the mentioned “magic” would prevail.
Still, one might think that we might be able to form new laws of physics, based on our empirical observations of just what happens in that world. Unfortunately, even that would be impossible. The reason is that we have and use the known laws of physics because they explain events, and such explanations are based on causality. Think of the earlier example of the gazelle and the lion. In the familiar, forward-running movie, we can answer the question “Why did the lion start moving toward the gazelle?” (i.e., what caused it to behave like that?) by pointing to the odor-carrying particles and noticing that they have a single source: the gazelle. There is a single source (the gazelle), and potentially multiple receivers (all lions in the region, including the one of our example, other gazelles, flies, etc). The idea of “single source, multiple receivers” is what allows causality to work. However, in the backward-running movie, the opposite is true: there are multiple sources and a single receiver (the gazelle), or “sink” of information, as it is called. When there are multiple sources we can’t point to a single one of them and say: “The event happened because of that”, because there is no rational reason to single out one of the multiple sources, since they are indistinguishable for explanatory purposes. The case of “multiple sources, single receiver” is what kills causality, and won’t allow us to formulate any rational set of laws of physics.
Actually, in a world without causality it’s not just that there would be no rationally formulated laws of physics. Something much stronger would be true: there wouldn’t be any sentient beings to think about anything — let alone formulate laws. The following section explains why.
3. The Loss of Cognition
The act of thinking, which is probably the most essential task of human cognition, requires memory. It’s impossible to conceive of human-like thinking without memory, either short-term, or long-term. The reason is that a thought is based on some things already existent, and these existent things reside in memory. For example, consider the thought: “It’s cold today.” In entertaining this thought, you are able to think it’s cold because you have a memory of recent past temperatures and an expectation of what the temperature should be according to them; the word “today” shows you’re comparing the present temperature with the past, and the past exists in your memory. Or, consider the thought “I’m feeling fine”: the mere act of saying “I” implies access to an internal symbol in memory that stands for your self, which is connected to (associated with) a vast collection of past events and objects in your memory. The totality of those associations allow you to identify the symbol with what you perceive as your “self”.[3] Subtract memory, and you wouldn’t “know thyself”, quite literally.
But what is a memory?
We have memories of the past and not of the future — that’s the one fact we know for sure. But are we alone in the universe with this ability? I am not talking about aliens, but about things here-and-now, around us: are human minds — and perhaps even a few animal minds to a much reduced degree — the only entities that remember things past? Well, now we have computers, you might say, which also manage to remember, and even more accurately than biological minds. But consider the world as it was for example before World War II, with no computers. What about then?
But, a “memory” of past events exists in the universe even without the aid of minds. Consider planets like the Earth, Mars, Venus (terrestrial planets, as they are called): the matter out of which they are made, the zillions of heavy atoms that form their masses, are a sort of “memory” of a large number of supernova explosions that happened in our galaxy before the formation of our solar system, because atoms with nuclei heavier than carbon can only be formed in the depths of stars that eventually undergo supernova explosions. (As is well known, even the atoms that form the molecules of our bodies have been manufactured in the depths of cosmic explosions.) Supernovas came first, terrestrial-like matter came later, as a consequence; the latter is a memory (of sorts) of the former events.
Or, take the asteroid belt in our solar system; it can be seen as a “memory” of a past event: the event of the collision of two astronomical bodies in the early stages of our solar system. Take the existence of mammals: it’s a “memory” of another catastrophic event, the event of the asteroid (or meteor) that stroke the Earth 65 million years ago and wiped out the dinosaurs (along with a large number of other species), thus paving the way for mammals to “radiate” evolutionarily and become the new conquerors of the “large terrestrial animal” niche. (The memory I am talking about is not in the mammalian brain of course, but in the fact of the existence of the mammals themselves.) Similarly, the existence of marsupials in Australia is a “memory” of the break-off of Australia from Antarctica, around 90 million years ago (actually from the super-continent Gondwana), thus protecting the marsupials from the invasion of placental mammals. Contrariwise, the existence of placental mammals in South America (and the near-extinction of marsupials there) is a “memory” of the joining of the two Americas at the isthmus of Panama, some 3 million years ago. (And so is the opossum, the only marsupial in North America, which migrated from south to north when the Panama land bridge was formed.) Our world is full of memories!