You Are About to DisappearOr: Why Time “Flows” but Space Just “Is”? |
Preface (and a warning)
Dear visitor, allow me to introduce myself. I am the great magician Harry Foudini, and my purpose in this text is to make you disappear. Yes, you read that right: it is wholly within my magic powers to make you disappear. But you’ve been forewarned: once you disappear, you won’t ever be able to come back; so it is entirely up to you to decide whether you want to continue reading this magic act. You are well aware of the “back” button on your browser, and if you are among the faint of heart, you are strongly advised to press it now, thus retaining your existence. I have spoken. If you keep reading, do not blame me for your subsequent non-existence.
So, with your consent, I proceed now with the magic act.
| In order to make you disappear, it will be necessary first to freeze the world; that is, to make time stop. Once time is stopped, your vanishing will proceed as effortlessly as you’d consume a piece of cake. So, sit back, and keep reading. |
However, it is not possible to reach immediately the time-freeze stunt without some preparation on your part. You’ll have to go through a series of simple mental exercises. This is what I will help you do next.
“People like us, who
believe in physics, know that
the distinction between past, present, and future
is only a stubbornly persistent illusion.”
Albert Einstein, March 1955
0. Introduction
You will first accustom yourself to the idea that your human cognition gives you a distorted, more complicated picture of the world than the one that really is out there. The examples listed in this introductory section aim at highlighting precisely this point: human cognition has the tendency to distort and complicate the physical picture.
0.1 Photons show us one thing, our brain sees another
The first example is one of distortion of brightness of light: the photons that arrive to your retina from two different regions of the external world have the same intensity (brightness), but your brain refuses to agree, for its own reasons. Look at the following figure.

Figure 0.1. The chessboard illusion: areas A and B on the board have the same shade of gray (due to Edward H. Adelson)
Take a look at the squares marked A and B, on the chessboard. Though your eyes tell you that square A is “black” and square B is “white”, in reality the shades of gray used to paint those two squares (not the letters A and B, but the background colors of those squares) are identical! Can’t believe it? You’re in good company: almost all people who encounter this illusion for the first time remain incredulous. The reaction of a friend of mine, when he first saw this figure, was to save the figure locally on his disk, then open it in the paint program of his operating system, and select a small piece of square A (a tiny rectangle from somewhere close to letter A), then drag and move the selected rectangle to square B. He noticed that the dragged small rectangle “disappeared” as it moved into B (because it blended perfectly with the color of that square — naturally, it’s the same color!). For your convenience, I’ve done this already on the figure above: you can see the two letters A and B extracted and copied on the lower-right corner of the figure, together with their backgrounds. You can see that — out of context — the two backgrounds now look identical. Another way to see it, if you still don’t believe me, is to take a sheet of paper (you need one that’s relatively opaque though) and poke two small holes one on top of the other, roughly at the distance of squares A and B. If you then cover up the figure with the paper, you’ll notice that the color that comes through the two holes is, magically, the same shade of gray. I suggest you try either of these two methods, in case you are not already familiar with this amazing illusion.
All right, so what is happening here? The light that reaches your retinas from squares A and B has exactly the same intensity. This means the same number of photons reaches your eyes per unit of time. The rods and cones (mostly cones) that receive these photons on two corresponding tiny spots of your retinas are excited in an almost identical way. So they send the same signal to your visual cortex, on the back side of your brain, both for square A and for square B. But what the visual cortex does with those two identical signals is another story. The visual system wants to see a checkered pattern of squares, on some part of which an object casts its shadow. So your brain automatically corrects the light intensities and mentally “subtracts” the shadow of the object, leaving the squares as they should be, i.e., black and white, in order to inform you that there is a checkerboard pattern there, which is shadowed in a diagonal fashion. Now, notice that your brain’s function is well justified. Imagine what the result would be if the brain couldn’t do that: instead of a checkered pattern with a shadow you would see the picture as it physically is, that is, as a diamond-shaped region with jumbled areas of various gray patches, some lighter, some darker, with diagonal bands close to its center (where at a higher level we perceive the shadow), plus some vertical bands with hues of green, a few of which form an elliptical region at the upper-right corner. What I just described is the “low level description” of the figure, one that any simplistic image-processing computer program can do as well. But what your brain does is not simplistic, but highly sophisticated image-processing, which allows you to see invariable patterns in the world (e.g., a checkered board), no matter how they are shadowed, occluded, twisted, brightened, darkened, color-bleached, color-saturated, or changed under a number of other visual transformations. It is vital that brains can do that. Or at least, it was vital — a matter of life or death — at some point in our evolutionary history, when our ancestors needed to be able to see and identify their prey and predators under a variety of lighting conditions. For our ancestors, those who possessed this ability, lived to breed and propagate this ability to their young, while those lacking or with diminished abilities, were prone to perish as they fell to predation or other misfortune.
But, evolutionary justifications aside, the fact of the matter is that in the case of the chessboard illusion, the photons give us one type of signal, but the brain interprets it differently, depending on the context. This is a case of cognitive “distortion”, where the human brain registers something other than what physical instruments (e.g., the photocell of a camera) would register. As you might suspect, the chessboard illusion is not a peculiar and isolated example, but a typical one, part of the brain’s cognitive arsenal. (By the way, if you enjoyed this illusion, consider visiting this page, which includes dozens more.) Now let’s see an example where the brain “complicates” the world (again for its own important biological reasons).
0.2 There are no colors in the world; our brains conjure them up!
When I was little I used to marvel at the orderliness and beauty of the rainbow colors. I had secured a crystal in the shape of a prism from the candelabra that was decorating the dining room ceiling of my parents’ home (always fearing that mom or dad would notice the missing piece, but somehow neither ever did), and was letting the sunlight pass through it, producing a beautiful bright rainbow pattern on the wall of my room. I was wondering, looking at the rainbow, if there are “more colors” than our eyes are able to see.
![]()
Figure 0.2. The visible part of the electromagnetic spectrum
Little did I know that, indeed, there are more “colors” — in fact, many more than those we can see — extending over a very wide range. This range is called the electromagnetic spectrum.
Light consists of photons, and one way to think of photons is as waves that travel in space. Each wave has a characteristic wavelength, which is the length between two successive peaks (or troughs — see figure, below). This length, the wavelength of photons — a mere number — is what we perceive as “color”. Red color consists of photons with a certain wavelength (around 650 nm, or 650 billionths of a meter). Yellow is photons with shorter wavelength (around 570 nm), green is shorter still (around 510 nm), and so on, all the way to fading violet, which is photons with the shortest wavelengths our eyes can see (around 400 nm). The following figure compares the wavelengths of three colors, exaggerating their lengths, but keeping the relative sizes to scale.

Figure 0.3. Wavelengths of three colors: red, green, and violet (drawn to scale)
But wavelengths do not end at the violet color just because our eyes can’t see photons with smaller wavelengths. Beyond the violet, up to around 10 nm, there is the ultraviolet, a “color” that is invisible to us, but visible to some insects, such as bees and wasps. (Also, some inconspicuous wild flowers that appear white to the human eye, actually reflect the ultraviolet color; and so, insects and flowers have co-adapted: the insects to be able to perceive this color, and the flowers to reflect it, so as to attract the insects.) The shorter the wavelength, the more energy the photon of that “color” carries. Thus the ultraviolet carries more energy than all the other colors of the visible range, and is responsible for tanning our skin when exposed to the sunlight. Overexposure to ultraviolet photons can burn our skin, but fortunately (and this is an important point for what follows) the ozone layer of our planet’s atmosphere reflects most of the higher-energy photons that roam in space (most of them produced by our Sun). Similarly, photons at the X-ray range (between 10 nm and 0.01 nm) have shorter wavelengths than the ultraviolet, and carry enough energy to penetrate soft tissues, making X-rays useful in medicine; but, as everyone knows, overexposure to X-rays destroys the tissues (much faster than the ultraviolet), and is lethal in larger quantities (causes cancer). Gamma rays have even shorter wavelengths (between 0.01 nm and 0.000001 nm, or beyond), are lethal, and most solid objects are nearly completely transparent to them (not the ozone layer, though). Some textbooks include the cosmic rays in the spectrum, although those are not really photons but extremely energetic particles that come from the outer space, and have a wavelength that can be even shorter than the gamma rays.

Figure 0.4. The entire electromagnetic spectrum (not to scale)
Wavelengths do not start with the red color either, as Fig. 0.4 shows. Larger-than-red wavelengths (up to 1 mm, i.e., millimeter) are in the “color” infrared, which is produced when we turn off the glowing red-hot range, as soon as the redness of the iron disappears, but while it is still warm. Any warm object actually glows in the infrared, including our bodies. That’s why mosquitoes can locate us in the dark: they can see in the infrared, so to them we are hot glowing objects (or rather, hot-served meal). Beyond that (with wavelengths of up to 10 cm) there are the microwaves (that make our microwave ovens work), and radio waves (making our radios, TVs, and cell phones work). If you want more information on the electromagnetic spectrum, and especially to see the visible range drawn to (logarithmic) scale within it, you can visit this Wikipedia page. Note that Figure 0.4, above, grossly exaggerates the width of the visible part within the electromagnetic spectrum: if the visible part were to be shown to scale, it would completely vanish, requiring a width of less than a single pixel to be drawn on our computer screens!
The preceding tour of the electromagnetic spectrum should tell us two key things: first, although the wavelengths of photons vary over a vast range, our visual system has adapted itself into perceiving only a small portion of it; and second, even within that part of the range that we see, although the wavelengths range continuously, our visual system has discretized the continuous range: it has broken it up into arbitrary and nonexistent pieces, those that we call “colors”.
This last idea is very simple: in the world, there are no colors, such as red, green, blue, and so on. There are only numbers that vary continuously, such as 400, 401, 402, and so on (and even between 400 an 401 there are the numbers 400.5, 400.25, and so on). But instead of perceiving a continuous range of numbers for wavelengths (similar to the way we perceive a continuous range of temperatures, say), we perceive entire regions of the spectrum that we label red, yellow, green, and so on. That we give names to colors is proof that we do this perceptual “discretization” (the breaking up into pieces). There is a region within what we call “green color”, for example (at wavelengths between around 490 and 530 nm), in which it is impossible for our visual system to see more than one hue of green; so we call that entire region “green”. (Note that scientists have broken up even the invisible part of the spectrum into discrete chunks, such as “infrared”, “ultraviolet”, etc., but for pragmatic reasons, unrelated to human perception.) Why do our brains do this? Why do they show us only a tiny part of a much greater reality? And why do they break up that tiny part of reality into pieces (the colors) that do not exist outside of human and animal vision?
There is again an evolutionary reason that explains why we perceive only one narrow band of the entire range: it is because the bulk of electromagnetic radiation emitted by our Sun that reaches the surface of our planet happens to be almost exactly in the visible range. Consequently, animals adapted to perceive photons in the range which is available, though some of them, as we saw (bees, mosquitoes), managed to explore the niches at the fringes of this spectrum, where photons are least abundant. The rest of the spectrum is either shielded by the ozone layer of our atmosphere, or is not produced by the Sun in as copious quantities as in the case of the visible range. No wonder we, animals on Earth, see only this tiny part of the range: we evolved to perceive what reaches us; we couldn’t possibly evolve to see what’s not available here, in this corner of the world where we exist.
There is also a physiological reason why we discretize the continuous visible range into chunks, the colors. It is because our cones (the photo-receptor cells on our retinas) are distinguished in three types, according to the pigment they contain: those with a pigment that receives mostly photons in the blue range, and then others with pigments for the green and red ranges. The intermediate activation of those receptors causes us to perceive in-between colors, such as orange, yellow, cyan, magenta, etc. (Variations in two other parameters, the luminosity of the color, and its saturation, result in colors that we perceive as pink, brown, white, black, and everything else.)
In other words, the conclusion of this subsection is that the physical world exists in some particular objective way (a vast continuous range of numbers, in the case of light), but our cognition forces us to perceive it in a completely different, subjective way (a much narrower range of discrete patches, the “colors”). So we need our physical instruments — and our knowledge of the relevant parts of physics — to realize the “cognitive deception” we undergo, daily.
Let’s continue to see how our cognition “deceives” us, with an example of a slightly more abstract nature.
0.3 The brain bends “straight lines”, turning them into circles!
First, before going into what the title of this subsection suggests, here is a straightforward example showing that human cognition tends to see something complex, when reality is actually simpler: consider the way the ancient peoples thought the planets moved through the sky. Thinking the Earth to be stationary, and at the center of the universe, they thought the planets had complex trajectories on the celestial sphere in the course of months or years, sometimes moving in one direction, other times decelerating, stopping, and turning around to move backwards. They thought so because in reality the Earth orbits the Sun faster than the outer planets (Mars, Jupiter, etc.), so at some point in the year it overtakes them, making them appear as if they move backwards. Also, the inner planets Mercury and Venus move faster than the Earth, which they do overtake within a single year. The ancient Greeks even found a mathematical model to describe all this complexity: it was Ptolemy’s theory of “epicycles” (2nd C. AD), which regarded the Earth immobile at the center of the universe, and the planets orbiting it, tracing what were thought to be “circles within circles”, or epicycles. Not all ancient thinkers thought so. The Greek astronomer Aristarchos of Samos (a.k.a. Aristarchus, ca. 270 BC) proposed that the Sun is at the center, and the Earth and other planets orbit the Sun; which is correct, but it was an idea too far ahead of its time to be considered seriously. Ptolemy’s “geocentric” (Earth-centered) model was making more sense, because it described what people’s eyes were actually seeing. The geocentric model was greatly simplified when the Polish priest and astronomer Mikolaj Kopernik (a.k.a. Copernicus, 1473 – 1543) rediscovered Aristarchos’s ancient “heliocentric” (Sun-centered) model, turning all planetary orbits to mere circles. The circles were to be slightly complicated later by the German astronomer Johannes Kepler (1571 – 1630), who found out they are ellipses, not circles, and once more later by Albert Einstein (1879 – 1955), whose general relativity showed that the ellipses actually rotate slowly; but even so, this was a great simplification compared to Ptolemy’s geocentric system; besides, Einstein’s “complexification” is only an apparent one: it is really a simplification, soon to be explained why.
A similar simplification occurred in the 17th century, soon after Copernicus’s re-establishment of the heliocentric system, when Sir Isaac Newton realized that the downward motion of any object pulled down by Earth’s gravity, and the circular-like motion of the Moon around the Earth, are really instances of the same kind of phenomenon. Both an apple that has ripened and falls from the tree, and the Moon, fall toward the Earth. It should be noted that Newton’s law of equality in action applies (both ways) so that the Moon also pulls at the Earth, perturbing its orbit slightly; the apple does so, too, but the degree is imperceptibe.

Figure 0.5. Simplification (generalization) of two types of motion initially considered distinct
(The figure above suggests and repeats the myth that Newton conceived of his simplification — or generalization — after sitting under an apple tree and receiving an apple on his head. No matter how far from the truth this legend is, I find that it has a certain educative value: it makes it easy for schoolchildren to learn and remember a deep idea, so I don’t feel any qualms about repeating it here.)
What I want to discuss, however, although it concerns planetary orbits, does not involve ideas that every schoolchild learns about, such as the straightforward simplification from the geocentric to the heliocentric model, or the generalization between the motion of falling apples and orbiting satellites. It’s about a simplification that most people do not come across, unless they study mathematics, physics, and/or astronomy. This simplification, which was possible only after Einstein’s general relativity, says that orbits of heavenly bodies actually are not circles, ellipses, parabolas, or other exotic curves (“conic sections”, as they are called), but... straight lines!
Did you think you know what a straight line is? At school we learn that a straight line is the shortest path between two points. This is fine as a definition, and it coincides with our intuitive notion of a straight line when the space is flat, like a 2-dimensional flat sheet of paper. However, if the space is curved, as on the surface of a sphere, then the shortest path that connects two points is not our idea of a straight line, because there are no straight lines on the surface of a sphere. The idea that comes to a layperson’s mind upon reading the previous sentences is that there still is a straight line that connects the points of the sphere: it is a straight line that starts at one of the two points, necessarily goes underneath the surface of the sphere, reaches up to a maximum depth at the middle of the distance, and then approaches the surface again and reaches the other point. But the problem with this idea is that this line must dive underneath the surface; it must leave the surface. When we say “the space is curved, as on the surface of a sphere”, we mean that the entire space is the spherical surface , there is no “out” to go, or dive into. Thus, if you are forced to stay on the surface of the sphere, what is the shortest path to connect two points? The answer is that it’s a line that looks like a “great circle”, or “equator” of the sphere. That is a “straight line” in that space, since it complies with our original definition: it is the shortest path connecting the two points. (Why is it the shortest? Because if you were to drive a car from one point to the other, you’d spend the least amount of gas, i.e., energy, if you traveled along that equator-like line connecting the two points; any other route would make you spend more gas.) To avoid confusion, instead of “straight lines”, mathematicians speak of “geodesics”, which coincide with straight lines as we ordinarily think of them when the space is flat; but on a sphere the geodesics are equator-like circles. Every surface, flat or curved, has geodesics.
Now, is our familiar 3-dimensional space flat? Until Einstein’s time, before he proposed his general relativity, people thought so; but in reality, our space is not exactly flat. It is approximately flat, especially in those places where massive objects are far away, but where massive objects — such as a star, our Sun for example — exist, space is curved in the vicinity of those objects. And when space is curved, “straight lines” (geodesics) are usually anything but straight, as we ordinarily think of the notion of straightness.
It turns out that the orbits of the planets are geodesics, but of our 4-dimensional spacetime, i.e., the continuum that includes the three dimensions of space plus the one of time, and into which everything that we know of in the macro-world exists. In that 4-dimensional continuum, planetary orbits are “straight lines”. Our cognition does not allow us to perceive all four dimensions as spatial (space-like), so what we see is the projection of the 4-dimensional orbit of a planet onto our familiar 3-dimensional space, on which it is distorted, and appears as an ellipse.
That projections can be distorted is something familiar to everyone. Think of the shadow of the trajectory of an airplane on the surface of the Earth (see next figure).
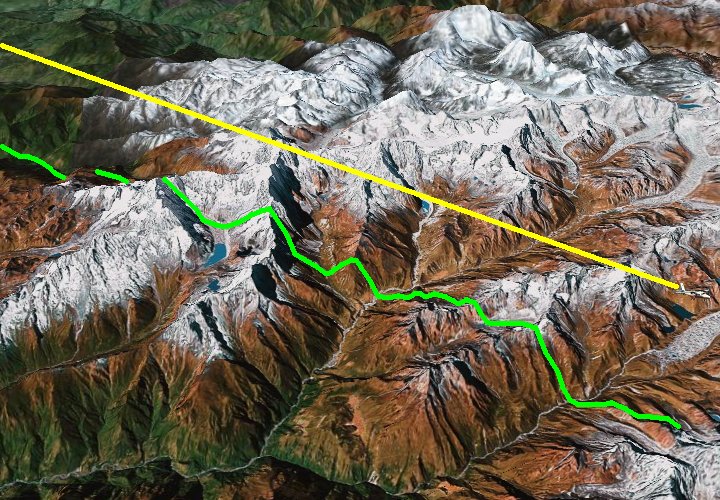
Figure 0.6. The trajectory of an airplane (yellow straight line) and its projection (shadow, green) on a mountainous landscape
Although the plane flies along a straight line in 3-dimensional space, its projection (that is, its shadow) on the 2-dimensional surface of the land(1) follows the ups and downs of valleys, plains, hills, and mountains. If we were unable to perceive the up-down as another (3rd) spatial dimension on an equal footing with the other two, but all we could see was the shadow of the plane on the 2-d surface of the Earth as it moves up and down, we would think that the 2-d trajectory of the plane is very complex. This is just what happens with the orbits of planets: we cannot perceive the fourth dimension (time) as just another spatial dimension, so what we see are elliptical orbits. However, if we were in a position to see four dimensions without our perceptual blinders, the orbits of the planets would appear just as straight as the airplane’s trajectory in three dimensions.
Example after example, we see the same pattern: although the world is simpler than we think, we evolved to perceive complexity, and it is only through the powers of the intellect that we manage to generalize and come to understand the underlying simplicity. In the case of the planetary orbits, too, there is an evolutionary reason that explains why we are built in such a way so as to perceive as space only three out of the four total macro-dimensions.(2) This evolutionary explanation is the main topic in what follows, by which the uniformity between space and time will be established, so that time will come to a standstill. Subsequently, you will vanish.
1. Time = Space
Let’s proceed to establish in the present section that time is essentially space, and that it is our cognition that complicates the picture, causing us to perceive the two as very different from each other.
1.1 The mystery of vanishing of “before” and “after” in physics
Physicists have long observed that, although our everyday experience tells us that the past is very different from the future, there is nothing in the laws of physics, as known since Galileo’s time, that points to some kind of asymmetry between the “before now” and the “after now”. Laws of physics are symmetric with respect to time. For example, Brian Greene writes in The Fabric of the Cosmos:[1]
“It turns out that the known and accepted laws of physics show no [temporal] asymmetry […]: each direction in time, forward and backward, is treated by the laws without distinction. And that’s the origin of a huge puzzle. Nothing in the equations of fundamental physics shows any sign of treating one direction in time differently from the other, and that is totally at odds with everything we experience.” (p. 13, emphasis in the original.)
What bothers physicists like Greene is this: they feel that if we, human beings, have some way of distinguishing between past and future, then there should be something in the laws of physics that shows that this is possible. But there isn’t!(3) For the typical physicist, the human brain is a physical mechanism, a device, a contraption abiding by the laws of physics, and this contraption apparently has some way of distinguishing between “before now” and “after now”. But why haven’t we discovered some physical law that also distinguishes between “before now” and “after now”, so that we can say, “Aha! Perhaps the human (or animal) brain uses this law, and that’s how it distinguishes between past and future!” Which physical law does the brain (the physical organ, the “contraption”!) use that we have not discovered yet? Isn’t this a puzzle?
Perhaps the reader might wonder what exactly is meant by the phrase “the laws of physics are time-symmetric”. Here is an explanation: Suppose you observe an object moving from point A to point B, at speed v = 1 m/sec. The object reaches B after 1 sec. Therefore, the distance between A and B is 1 m. The formula that relates space s, time t, and speed (or velocity) v, is known since Galileo’s time and we learn it in high school: s = v·t (substitute v = 1 m/sec and t = 1 sec to find s = 1 m). Now, what would happen if this event was run “backwards”? That is, what if time was running in the reverse direction, like an old-fashioned movie in which the direction of the film has been reversed, showing people walking backwards? Nothing essential would change in the physics event. We would see the object going from B to A, instead of from A to B. To describe this we would use the same formula s = v·t, and we would have the option of putting t = -1 sec, and v = -1 m/sec, (since v comes with an arbitrarily set positive direction, which in this example we took it to be from A to B), yielding again s = 1 m. No essential change was made. To put it otherwise: if we see a movie showing an object going from A to B, and another one showing the object going from B to A, we have no way of knowing which of the two movies was shot in time running forward, and which in time running backward.
The savvy reader might have thought, at this point, that there is indeed a number of events that take place in the macro-world (i.e., the world of our everyday experience) that seem to be irreversible in time. For example, whole eggs break, but nobody ever saw the pieces of a broken egg to come miraculously together, forming again a whole egg. The law of physics that describes such events is the Second Law of Thermodynamics. But that is a statistical law, not a fundamental law of physics in the same sense as s = v·t is. Indeed, the fundamental laws of physics predict that there would be nothing miraculous if we should see a broken egg forming back into a whole one; it is the laws of probabilities that place a vanishingly low value to the probability of such an event happening. But the fundamental laws of physics are mute when it comes to broken eggs. (Read this page of mine to understand why the second law of thermodynamics is not a law of physics, but a purely mathematical result; i.e., it requires no experiment, no observation of nature in order to state and understand it, only the statistical manipulation of some geometric formulas.)
All right, so “that’s the origin of a huge puzzle”, according to Greene. We shall see later in this text that, indeed, correctly it is a puzzle for physicists, because time’s asymmetry and especially its directionality(4) is not something that can be explained strictly within the domain of physics, no matter how awkward this sounds. Time’s asymmetry is a statistical effect of the second law of thermodynamics (this is well understood by physicists), while its directionality is a psychological (cognitive) effect(5) (this is not well understood; I discuss the explanation for the directionality of time in this page). So, what appears as a puzzle to Greene is so, because what he asks is not a question for physics, but for cognitive science. This is at the crux of what the rest of this text will attempt to explain.
1.2 Been at two different places at the same time? Anyone?
I would like us to think seriously how the facetious title of this subsection can be satisfied. But before we can think how something can be at two places at the same time, let’s think of a much simpler achievement:
Can something be at the same place at two different times?
Oh, come on, this is trivial. It is done all the time by any object that starts off at location A at time t0, then goes a bit further up to some location B, where it stops, changes direction, and comes back to A at time t1. Every baby who learns to walk can do it. Why did we have to do this trivial exercise?
Because although every baby can do it, no adult, no matter how well equipped technologically, can do the opposite: to be at two different places at the same time.
Of course not. For material bodies this is forbidden by relativity: one would need to move at the speed of light to be able to go from A to B at the same time t0 (according to the moving object’s frame of reference), and no object with nonzero mass can do this, because an infinite amount of energy would be required to accelerate the object all the way to speed c; and infinite energies do not exist.
Exactly, a material object wouldn’t be in a position to achieve this. But what about a non-material particle? Say, a photon?
A photon is not an observer, though.
We did not require that it must be an observer who can be at two places at the same time. So, it seems a photon can do it. But if we insist to have an observer, how about relaxing the requirement that the time t0 must be exactly the same? What if we ask that something, an observer, be at two different places within a very short interval of time, Δt?
That doesn’t seem to be problematic at all. Provided, of course, that if Δt is very small, and the space-like interval A-B sufficiently long, then the corresponding speed of the observer must be very high, very close to c. And its kinetic energy must also be high, assuming the observer possesses some amount of mass.
So, that’s it. We can have observers who, when moving at very high speeds (close to c), manage to be at two places at almost the same time (according to their watches). Let’s imagine such a hypothetical world of fast-moving observers, and try to figure out what space and time would look like from their perspective.
1.3 The world according to plasmoids
In this subsection we’ll try to understand our perception of the properties of the world we inhabit by building an analogy with a hypothetical world, a world that consists of energetic particles, and is inhabited by cognitive beings that run at nearly the speed of light with respect to landmark objects in space (e.g., the stars). For the sake of avoiding circumlocutions, I’ll call these beings plasmoids.(6) Thus, plasmoids move in one direction in space against the distant stars (suppose their spatial world consists of a single dimension) at nearly the speed of light, c. We assume they have evolved in this world (i.e., in our universe), and the question is what the world appears to be like from their cognitive perspective.
If plasmoids move in space at speeds nearly equal to c, space must appear to them to be “flowing” in one direction. If their velocities are assumed to be always very close to c, then their perception could possibly include the feeling that they do not have any control on the passage of space. This is because tiny fluctuations around their “normal” velocity, c, would be imperceptible by them. Why? Because having evolved in a world where velocities are always very close to c, plasmoids would not have developed sensors for the very slight differences in the speed of the passing space, because such differences, being minute, would not help them to be naturally selected against other species in their environment. The way to understand this is by reversing the analogy and applying it to our familiar world. We, animals on planet Earth, did not develop sensors for the differences in which time flows, because — due to our extremely slow speeds with respect to c relative to our perceptible surroundings — such differences do not provide a survival advantage. Yet, they exist: the clock of a human observer that moves on the surface of the Earth runs slightly slower than a synchronized stationary one. Those differences are so tiny, however, that it is not biologically possible for an animal to evolve such detectors and use them for its own advantage.
There are numerous such examples in the biological world. Take, for instance, X-ray vision. Although the bulk of electromagnetic radiation that reaches the surface of the Earth is in the visible range, as we already noted in §0.2, there is a minute amount of radiation from all the rest of the spectrum, including X-rays. Conceivably, it would be advantageous to be able to see in X-rays — animals with such visual systems would be able to see through objects that to other animals appear opaque. Nonetheless, just because X-rays are advantageous does not mean a biological mechanism must have evolved that exploits this niche. Not every physical feature constitutes a biological possibility.(7) Just as no creature evolved to see in X-rays, similarly, no creature on our planet evolved to perceive minute differences in the speed of the flow of time. Analogously, it seems reasonable to assume that the plasmoids of our thought experiment lack the ability to sense minute differences in the flow of space.
Now, one may claim that plasmoids could still have developed such sensors. We, after all, do have motion-detectors in our brains, sensing the slightest motion (change of coordinates) of objects in space; therefore, why should plasmoids lack a similar mechanism if such mechanism is demonstrably physically possible? The answer is that we humans compare the new spatial coordinates of moving objects against zero, i.e., the relative immobility of other nearby objects; while the plasmoids would have to sense a difference in spatial coordinates against a background of coordinates that change at the rate of the speed of light, c — which is a large(8) constant. Any small deviation from c is “drowned” by the magnitude of this constant, which makes the detection of such deviations difficult. It would be like trying to detect a whisper near the working engine of a jetliner. The reader might think, however, that c appears large only to us, while for plasmoids it may, in a symmetric way, play the role of “zero”. But c is objectively different from zero: it is the constant that defines simultaneity in our universe, through the relation s = c·t; and also the constant that defines the equivalence of mass and energy, through E = m·c2. Zero, apparently, does not possess such properties.
Assuming that plasmoids did not evolve mechanisms to perceive the minute differences in the flow of space, what about their perception of time? Would plasmoids feel they can navigate back and forth in time, as we have the analogous feeling for space? To allow the “backward” motion in time — although by a very small degree — we need to assume an additional feature for plasmoids. Normally we, human observers, perceive ourselves as consisting of a large amount of inert mass, and very little kinetic energy: we perceive ourselves as being usually stationary relative to our environment. We can, however, produce some kinetic energy by spending a tiny amount of our mass (a process carried out in the mitochondria of our cells), and by so doing we feel we can move in space in any direction, although at very slow speeds relative to c. Likewise, plasmoids might convert a tiny amount of their kinetic energy into inertial mass (henceforth called simply energy and mass, respectively, dropping the adjectives for simplicity), thus slowing down their pace, slightly. However, their metabolism also allows them to do the reverse: decrease their mass down to zero, converting it all to energy, thus moving at exactly the speed of light. (By analogy, we can decrease our energy down to zero, coming to a standstill.) Moreover, they can pass on the “other side” of the mass–energy spectrum, acquiring a very small amount of imaginary and negative mass and energy, and a speed slightly greater than c.(9) That they acquire such exotic properties as imaginary and negative mass and energy is a consequence of the relativistic formula:
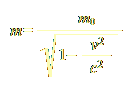
where, if v > c, the quantity in the denominator becomes imaginary, so the fraction becomes analogous to m0/i; and since 1/i = -i, we obtain an imaginary and negative m. Energy follows suit, due to E=m·c2. Now, to understand how plasmoids manage to achieve small displacements in time, it is helpful to consider how we perform displacements in space. We do this by moving from one location to another, measuring the time t (which we do not control) it takes to do so. The quotient of space s over time t, we call velocity.(10) Similarly, plasmoids could decide to move “forward” in time (relative to the time-frame in which they currently are) by increasing slightly their mass, hence decreasing their energy and speed — all the while staying in the vicinity of c and of the maximum energy(11) they can obtain. They can accelerate by decreasing their mass. When mass becomes zero, they achieve their maximum energy and speed c, and they can then move slightly “backwards” in time by accelerating further, obtaining imaginary–negative mass and energy — always staying in the vicinity of c. Note that if plasmoids cannot physically distinguish between normal and imaginary–negative mass and energy, they also perceive a perfect symmetry between “forward” and “backward” motion in time; to them, it is simply motion in this or that temporal direction.
1.4 Could time dilation and space contraction save the day?
So far we have been building a point of view in which the notions of space and mass are in complete symmetry with the notions of time and energy. It all seems to depend on which side of the mass–energy spectrum you happen to have most of your existence. But what about the relativistic notions of time dilation and space contraction? Don’t the different notions, dilation vs. contraction, as first described in Einstein’s seminal paper,[2] point to a fundamental difference between space and time? After all, time dilates, it doesn’t contract; instead, the notion of contraction applies to space, and since dilation and contraction are opposite to each other, don’t they give us a means by which to tell which dimension is space, and which time? Perhaps we are able to say that the dimension that is dilated is the time, whereas the one that is contracted is space. In this sub-section we’ll find that the symmetry between space and time persists, i.e., what appears to us as dilation, should appear to plasmoids as contraction, and vice versa. (If you are reluctant to follow the technical details below, you can trust me that the symmetry persists and skip to the next sub-section.)
Let us consider the concepts of dilation and contraction from the plasmoid perspective. As mentioned, plasmoids do not directly perceive motion in space. Nonetheless, their physicists can assure lay-plasmoids that their instruments measure a “dilation (or expansion) of space” for every observer O2 who changes their time-coordinates with respect to another observer O1. Here is why.
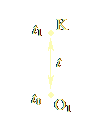 |
 |
| Figure 1.1a | Figure 1.1b |
Consider plasmoid-observer O1, whose time-coordinate is t0 (Fig. 1.1a). O1 sends a photon towards event K. The photon travels for a total time of t (from O1’s perspective), is reflected upon reaching event K at time t1, travels back, and reaches O1 at the same time-coordinate t0 (because O1 stays immobile in time). O1 computes that the photon traveled for a total time-distance 2t. Therefore, the space s that passed while the photon made this trip is s = 2ct. Now consider Fig. 1.1b, which shows the same sequence of events, but from the point of view of a second plasmoid-observer, O2, who moves uniformly in time with respect to O1, and who, therefore, perceives O1 and K to be changing their time-coordinates at a uniform rate, as space goes by. O2 notices the photon leaving O1 at time t0, reaching K at time t2, after having traveled for a total time-distance t' > t, being reflected at K, and returning to O1, who is now at a different time-coordinate, t3. The total time-distance according to O2 is 2t', which is greater than 2t. O2 computes the total space that passed from the location of the first event at t0 to the location of the second event at t3, and finds it equal to s' = 2ct' > 2ct = s. Thus O2 computes a larger value s' > s for space, and claims that the moving observer O1’s space is “dilated”.
If plasmoids observe space dilation, then, by symmetry, we expect them to also observe time contraction. Indeed, suppose plasmoid-observers O1 and O2 are moving at the same speed v towards a third plasmoid-observer, O, who wants to compute the difference in space coordinates between O1 and O2 (Fig. 1.2a).
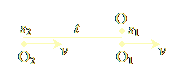 |
 |
| Figure 1.2a | Figure 1.2b |
Suppose O1 arrives first at O’s time-coordinate t0, so O marks the spatial coordinate s1 of O1 when they are both at the same time-coordinate. A short space afterwards, O2 arrives at O’s time-coordinate (always t0), and O marks the new space s2 where this meeting took place. O computes the total time-difference between O1 and O2: t = (s2 - s1) / v (Eq. 1). Now consider the situation in Fig. 1.2b, which is similar to the one in Fig. 1.2a, except that now, it is O who is moving at speed v, and is traveling from the time-coordinate of O1 to the time-coordinate of O2, intending to measure their mutual time-difference. O is at O1’s time-coordinate at space s1', and arrives at O2’s time-coordinate at space s2'. O computes the total time-difference between O1 and O2 as: t' = (s2' - s1') / v (Eq 2). From eqs. 1 & 2, eliminating v, we get: (s2 - s1) / t = (s2' - s1') / t', hence: t = t' (s2 - s1) / (s2' - s1') (Eq. 3). We saw in the previous paragraph that O’s space must be “dilated” in the situation of Fig. 1.2b, so we conclude that s2 - s1 < s2' - s1'. Hence, from Eq. 3, we conclude that t < t', which means that O observes the time-difference t of observers O1 and O2 in Fig 1.2a to be “contracted” with respect to their difference t' computed in the inertial frame of Fig. 1.2b.
The previous results are, of course, predictable from the exchange of roles between the concepts “space” and “time” in the world of plasmoids. What this subsection shows is that even such concepts as our familiar relativistic time-dilation and space-contraction do not in reality point to any fundamental difference between space and time. What we call “dilation” the plasmoids would call “contraction”, and vice versa. There is no attribute that can be attached to either space or time, distinguishing one from the other.
What we call “space” and what we call “time” are relative notions — that’s the final conclusion; relative, that is, to the mass–energy constitution of the observer.
1.5 Could it be that we are really cruising through time?
The hypothetical world of plasmoids tells us that even if the spatial and temporal dimensions of our world are objectively similar to each other (as the laws of physics inform us), the way they are perceived by cognitive beings existing in those dimensions depends on the particular relation that such beings have with each dimension. Plasmoids, living in the energy-rich end of the mass–energy spectrum, hypothetically evolved to perceive small displacements in time, but to feel that space passes by, in an inexorable march from locations yet to be encountered, to locations left behind. Human beings, living in the opposite, mass-rich side of the spectrum, evolved perceiving small displacements in space, but feeling that time passes by, in an inexorable march from events yet to be experienced to events left in human memory.
A question that can be asked at this point is the following: if plasmoids move in space relative to spatial landmarks, couldn’t we be thought of as “moving in time”, and at nearly the speed of light, c?(12) Let’s see what the experts have to say on the matter. According to Greene,[1]
“Special relativity declares a [...] law for all motion: the combined speed of any object’s motion through space and its motion through time is always precisely equal to the speed of light. At first, you may instinctively recoil from this statement since we are all used to the idea that nothing but light can travel at light speed. But that familiar idea refers solely to motion through space. We are now talking about something related, yet richer: an object’s combined motion through space and time. The key fact, Einstein discovered, is that these two kinds of motion are always complementary. When the parked car you were looking at speeds away, what really happens is that some of its light-speed motion is diverted from motion through time into motion through space, keeping their combined total unchanged. Such diversion unassailably means that the car’s motion through time slows down.” (p. 49, emphasis in the original.)
Thus, assuming that our motion through space is not all that great (we follow the motion of Earth, which orbits our Sun, which orbits the galactic center of our Milky Way galaxy, and so on), it follows that our motion primarily takes place in the dimension of time.
I must note here that a physicist, reviewer of an earlier draft of this document (in which the above excerpt from Greene was not included, only a reference to it), had a gut reaction against the idea of “motion through time” and scoffed at it. For that physicist, motion is associated with the concept of speed, and speed is the quotient of space over time, so motion happens necessarily in space. How can we conceive of motion in time? What would be the speed of something moving in time? We cannot divide time over time to find the speed (or if we do we get nonsense), so the entire idea of motion in time is nonsense, according to that physicist.
And yet, what is missing is, I believe, a tiny bit of mental effort to generalize from the concept of speed as we learned it in high school (the quotient of space over time), to a generalized concept, call it “rate of spatiotemporal motion”, or “rate” for short, which includes both our familiar speed (space over time) and its inverse notion (time over space). Rate has a dual nature: when expressed in our terms (from our human perspective), it is our familiar speed; but when expressed in plasmoid terms, it is the inverse notion: time divided by space. Mathematically, we can represent it by the pair [v, u], where v is our familiar velocity (speed, or: space over time), and u is the unfamiliar temporal component (time over space). The larger v is, the smaller u becomes, and vice versa, so that v + u = c is always true. Rate is of course relativistic, so it depends on the observer, and its two components are bounded by the speed of light, c: one extreme value for rate is [c, 0], and another extreme value is [0, c]. Thus, if we observe a plasmoid moving at c (mass zero, energy highest), the rate of that plasmoid is [c, 0]. Similarly, if we are immobile with respect to landmark objects (stars), we have a rate of [0, c]. Perhaps there is some better, more productive formalism for this notion of “rate” — because, honestly, I don’t see how one can do useful physics with a mathematical pair — but the existence or non-existence of a better formalism is not an argument against the existence of the concept itself, i.e., rate, as described above. Note that the use of the word “motion” in this context is misleading. There is really no motion; only a sequence of 4-d points (“events”) in 4-d space–time.
So, the question “What is our speed in time?” does not make sense if by “speed” we mean the familiar concept. But we can ask, “What is the temporal component of our rate when we are immobile with respect to the stars?” Assuming that by “temporal component” we mean the second element in the above pair of the representation of rate, the answer is that our temporal component is c.
A way to visualize the above, which is quantitatively wrong but qualitatively right — we’ll see in a moment what this means — is given by the following analogy. Suppose we have a 2-d space like a sheet of paper, infinite in all directions, and instead of naming the dimensions x and y as usual, we name them s and t (see Figure 1.3, below). Draw a vertical straight line segment, as in Fig. 1.3 (a).
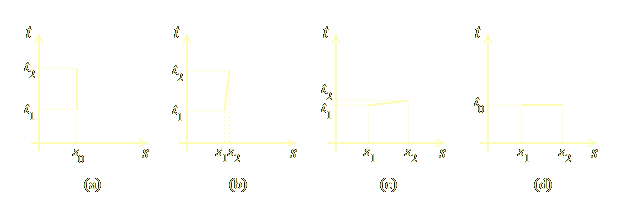
Figure 1.3. A simplification of the notion of motion in spacetime
The vertical line segment in Figure 1.3 (a) corresponds to a point that stays stationary (with respect to the stars) for some time, from t1 to t2. Since it traverses no interval in space, its spatial coordinate is fixed, at s0. Figure 1.3 (b) shows a point that moves at a slow speed, so it traverses a small interval of space between s1 and s2, during a larger interval of time between t1 and t2. Notice that what remains fixed is the length of the straight line segment. In Figure 1.3 (c) we see a point that moves very fast in space, approaching the speed of light (a plasmoid of very small mass, say), so now the space-like interval s1s2 is large, and the time-like interval t1t2 is small. Finally, Figure 1.3 (d) shows a point that moves at exactly the speed of light (a plasmoid of mass zero), which traverses a certain length in space s1s2, in no time at all, i.e., it exists at two different locations at the same time (t0).
The concept of familiar speed, in the above analogy, corresponds to the angle of the line with respect to the temporal axis, t. Thus, in Fig. 1.3 (a) the inclination is zero, hence the speed of the point is zero. But, correspondingly, the dual notion of “temporal component of the rate” of this point is the angle of the line segment with respect to the spatial axis, s, and so it has its maximal value. In diagrams (b) and (c), the first angle (spatial component, familiar speed) is increased, and the temporal component (dual notion of speed) is decreased, finally becoming zero at (d). The speed of light, c, corresponds to an angle of 90° in this analogy.
What is wrong in Figure 1.3 is that it pretends that the space is Euclidean (flat), i.e., that the length of the line segment remains invariant as the segment is rotated on the plane. But spacetime in a special-relativistic world is not Euclidean, but Minkowskian (“hyperbolic”), which means that the length of the line segment would change somewhat as it rotates, if we measure it with one of our familiar rulers; but if we measure it with a “hyperbolic” ruler, suitable for Minkowskian geometry, then the length would turn out again to be fixed, and its square would be equal to s2 – t2. (Alternatively, you can imagine that the space depicted is not flat, but warped in some way.) That’s why we cannot use Figure 1.3 to make quantitative measurements: because the space shown is not our familiar Euclidean one. But, qualitatively, i.e., as a mere analogy, Figure 1.3 is right: it gives us a visual way to understand the notions of familiar speed and its dual concept (analogous to angles, with the property that increasing one causes the other to decrease), and of the idea that no matter how fast an object moves in space, there is something invariant about it: it’s the length of the line segment, if measured with a suitable ruler in the proper geometry.
1.6 If time = space, how come there is no formula in physics noting this?
But there is! Here it is:
s = c · t
Everybody knows it, but few people take it at face value for what it really says.
The factor c in the above formula is a constant. It is there only because we use our parochial units for measuring space and time; specifically, the meter (m) and the second (s), so we say that c = 299,792,458 m/s (meters per second). But our choice of units is arbitrary. We could equally well be using the light-year as the unit of space, and the year as the unit of time, in which case we would have c = 1 (light-year per year), and then the above formula would be written:
s = t
which says precisely that space and time are the same “stuff”.
A way to derive the formula s = c·t is the following. Suppose there are two locations in space, s1 and s2. Suppose also that at time t1 a photon starts off at s1, moving in the direction of s2, and reaching s2 at time t2. Then the events (s1, t1) and (s2, t2) are called simultaneous, and the relation that holds between the space and time intervals is: (s2 – s1) = c · (t2 – t1); or, if we omit the indices, we can write simply s = c·t. The meaning of this formula is that every quantity of time corresponds to an equivalent quantity of space. For example, it tells us that one second of time is equivalent to 299,792,458 meters of space. If instead of a photon we use a material particle that moves at speed v in the above description, then we get the formula s = v·t, familiar from high school physics.
2. The Magic Act (by Which You Disappear)
If time is really like space, as suggested in §1, and if the way time and space are perceived depends on the physical constitution of the perceiving cognitive agent (if made of mainly mass, then time flows and space is; if made of mainly energy, then space flows and time is), then the picture of the universe that emerges is one of a “frozen” world, which some scientists have dubbed, appropriately, “block world” (e.g., Dickson[3] pp. 165 – 174). In such a world, every event that happened or could possibly happen is already there, laid out in the four-dimensional space-time continuum.
Let’s repeat this, depicting it in a drawing, because it is of central importance for the stunt of your disappearance. Look at the following figure, a repetition of a part of Figure 1.3:
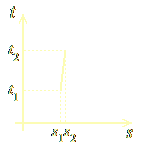
Figure 2.1. Spacetime as block world: a point moving, or a frozen line?
What does Figure 2.1 show? From one point of view, it shows a point moving from location s1 to location s2, doing this between the corresponding times t1 and t2. But from another point of view, it doesn’t show any motion at all; it merely shows a line that just stays there, doing nothing; a frozen line. And, just as this can be done for points in uniform motion, it can be done for any familiar 3-d object, including yourself (and myself, and anyone else). Instead of busy creatures, moving about in space, we can imagine ourselves as frozen objects in 4-d spacetime. We don’t really act, we don’t move, we don’t do anything in 4 dimensions, we just are, according to this alternative view.
But something is amiss. If time is exactly like space, if our world has four identical dimensions, why is it that there is a distinction between that dimension (time) and the other three (space)? This distinction must be objective, independent of human cognition, and here is why: imagine an observer that comes from “outside” of our universe (ignore for a moment that we don’t know whether such an outside exists) and takes a look at our universe from afar (ignore also the cognitive properties that this observer should have). So, the observer “perceives” our world, and says, “Aha! There are some 4-d beings that possess mainly mass, and their 3-d projections think this dimension is flowing and the other three just stay around.” Why is the other-worldly observer in a position to discern one of the four dimensions (time) and single it out as special?
The answer is that there is an objective difference between time and space. But I am not going to go into that topic now because it is irrelevant for the purposes of the disappearance stunt. The difference would be of interest to philosophers, if they could ever be interested in any idea that has not originated from within their own intellects. In any case, the difference is outlined in the first objection in the Feedback section (§4), and explains why we find ourselves on this side of the energy–mass spectrum (i.e., possessing a lot of mass and hardly any kinetic energy), why we couldn’t be on the other side (little mass, much energy), and why the geometry of our world has to be relativistic, not Euclidean. But, as I said, who cares about all that. We are interested in the disappearance stunt. Are you ready?
Suppose for a moment that the alternative view is the “correct” one, i.e., time is just another spatial dimension, extremely similar to the other three ones (though it can be distinguished geometrically), and it is only our cognition that’s responsible for “complexifying” the picture, making time appear so different; in reality, nothing moves, nothing changes, all is frozen. Thus, we could even reverse the famous dictum by the ancient Heraclitus:(13)
| Everything stays, and nothing flows. |
Now, if nothing flows, what about your own thoughts? They must be frozen, too, correct?
“Frozen thoughts” means mental patterns that exist both before and after the “now” (which is a mere illusion of your 3-d self). Consider the analogy of such thoughts with the “frozen music” in the grooves of an old-fashioned LP disk (or even on a modern CD, except that the “grooves” on a CD cannot be seen with the bare eye). Music sounds like music as long as a reading device (e.g., a needle, a laser beam) moves along the grooves. But if there is no such reading act, if all you have is the totality of the grooves on the disk, this doesn’t give you the feeling of music, does it? In a similar vein, if time is frozen, your thoughts do not look very much like thoughts anymore. For one thing, your future thoughts are already laid out. The “now” of you (your 3-d self) doesn’t know your future thoughts, so they appear as if you haven’t entertained them yet. But in reality — in the frozen reality — your 4-d self has them all figured out. Consequently, you (the full 4-d of you) are not thinking. You think you are thinking, but you are deluded. Your delusion stems from your having the perception of a 3-d slice of yourself at any moment, and retaining in your memory some representations of your earlier slices. But in the 4-d of you — all of you — there are no such temporal slices, only one continuous, long 4-d “chunk” of you, from birth to death. And this “chunk” is not thinking any thoughts, just as an LP or CD that’s seen all at once is not playing any music.
But if your 4-d self is not thinking, it follows that...
| Cognition itself is an illusion. |
What sense, then, does it make to say that you “exist”? Existence can be conceived of only in time: something can be here now, and continue to be here (or there) a little later, so we say it keeps existing between these two times. If time does not flow, if it has the quality of space, then what sense does it make to say that anything “exists”? Also note the phrase “Existence can be conceived of...”, above; if cognition is an illusion, how can anything be “conceived of”?
| Corollary: You do not exist. |
All right, this concludes our disappearance stunt. But let’s make a few thoughtful steps further.
If your thoughts, including your future ones, are all laid out in the 4-d spacetime continuum, then you don’t really decide anything by your own free will. You have the illusion that you decide, because your “now”-snapshot is uninformed regarding your future snapshots. But who cares what your “now”-snapshot knows or doesn’t know. Your future decisions are all laid out, so...
| Free will, too, is an illusion. |
“A!... But wait!” I hear you saying. “Even in the face of all these bleak conclusions, there is one rock that remains unmoved, untainted by your vulgar attack on the human condition: it is God! God stays out of all this dead material 4-d (or whatever-d) world; God is the one who can observe us and know our future states, because, unlike us, God does not see only snapshots, but our entire 4-d selves, past, present, and future.”
Slow down, not so fast. I’m afraid news are not so good for your God, either. Did you say, “God sees”? Well, not with some pair of eyes, I suppose, right? But then you must mean that God perceives something, correct? God knows things, yes? (Isn’t God the omniscient type of fellow?) But if God knows anything at all, God must have cognition. It’s not possible to claim that God is omniscient, perceives and remembers things (and even listens to prayers and issues judgments, as many people believe), and insist that God is not a cognitive being! You can’t have your pie and eat it, too — if you do, then admit that you are a little irrational cheater! So, if God is a cognitive being, then...
| God does not exist, either. |
Naturally so, I would add, because it seems to me that God is a creation of the human intellect, and as such, suffers from the same flaws that plague the human intellect as a whole. But it really is of no import what I believe about God, because the above corollary is independent of my personal opinion. It simply says that if God knows anything, then, by virtue of being cognitive, God does not exist, since no cognitive being exists (“cognition is an illusion”, see above). Otherwise, if you insist that your God exists, then you must admit that your God is not a cognitive being, i.e., does not know anything. (I repeat the same idea in different wordings because I am painfully aware of the inability — or reluctance — of religious people to use and apply ordinary reasoning when it comes to matters of their faith.)
2.1 Impossibility of time-travel into the past
Let’s draw one last logical corollary from the above. There is a favorite and continually recurring theme in science fiction: time travel. Since the days of H. G. Wells’s The Time Machine (1895) people keep reading about other, fictional people, who travel back and forth in time. And it’s not just science fiction, sometimes it’s science, too (or at least it is thought to be). In a special edition of the Scientific American devoted to the subject of time, an article seriously considered the possibility of time travel, and it was not an isolated occurrence of this idea in that magazine. But if everything stays and nothing flows, in what sense is time travel possible?
I must point out immediately that there is some sense in which time travel into the future is possible, and in more than one way. For example, one might enter a state of deep freeze, and be unfrozen by superior technology in the future, as is attempted in the field of cryonics; alternatively, one might travel sufficiently long and with sufficiently high speed, and upon return discover that a lot more time has elapsed at the departure and arrival place than by the traveler’s watch and biological aging rhythms, as relativity predicts. None of these methods of travel into the future contradict the above ideas. From a 4-d perspective, a 3-d being who performed this kind of “time travel” is merely a being with a portion of its existence that appears time-wise uniform (see following figure).

Figure 2.2. Two ways to extend an ordinary existence (top): the “cryonic” (middle) and “relativistic” (bottom) dreams
The figure above shows two possibilities for something that could be regarded as “time travel into the future”. The drawings are abstractions. The top one shows an ordinary life, with its “ups and downs”, time running from left to right. In the middle drawing, life enters a frozen state at some time, during which nothing happens, and later it is “thawed” and continues normally. The bottom drawing shows a life that proceeds normally up to a certain time, when it embarks a fast-moving spaceship, travels sufficiently long in space, and returns to its point of departure, thus slowing down its biological rhythms substantially.
There is nothing impossible about the described situations (though there are lots of things improbable, at least by today’s technological standards). Indeed, the drawings above can be seen as showing the beings in their entirety, i.e., laid out in time. The only observation worth making then is that some of the above beings have a piece of their existence that’s substantially different from the rest of their existence: if we trace it along the temporal dimension (in either direction!) we see that it appears to be relatively uniform — and that’s all.
But time travel in science (fiction) usually does not involve any of the above kinds, but a kind by which the traveler returns to the past, and might even meet his/her own earlier self to boot. According to the above, this is a logical impossibility. A “traveler” is a 3-d snapshot in time of the entire 4-d existence of a being. But a 3-d snapshot does not travel, it merely is; it just stays next to other snapshots along the temporal dimension. How can a 3-d snapshot of a being be moved anywhere in time in a static picture? No motion of 3-d snapshots is possible; one can only observe different 3-d snapshots, all waiting there, in 4-d spacetime. Nothing moves, nothing time-travels. There is only a tangential possibility: that one of the 3-d snapshots of the being acquires in its memory the perception of a world in which it appears to an earlier 3-d snapshot of itself, in some sort of virtual reality. But this is usually not what science fiction writers imagine. Therefore,
| Actual time-travel into the past is an absurdity. |
2.2 Why should anyone consider at all the “Time = Space” idea?
A friend of mine, after undergoing the above disappearance stunt, refused to disappear, on the following grounds:
“Why do I have to accept the view that time and space are really one and the same thing?” my friend asked. “I could just as well imagine that time is just as I perceive it: a succession of ‘nows’, and my existence passes through these ‘nows’, leaving behind the ones I already experienced, knowing that I will meet ahead the ones I haven’t experienced yet. What’s wrong with this view?”
There is something inherently wrong with this view, which I am going to discuss in the 3rd objection in the Feedback section (§4). But at this point I would like to pretend for a moment that there is nothing inherently wrong with it, because even then we can make some interesting observations.
So, let’s see: similarly, there is nothing inherently wrong with the geocentric model, or with the perception of colors, or with thinking that the orbits of planets are really ellipses, or other conic sections. Sure, for each one of these views a case can be made arguing for the need to keep the view alongside its alternative one. There is no a priori logical reason why the more complex views should be abandoned in favor of the simpler ones. Indeed, in practice we do keep some of those views around. For instance, although we know that there are no colors in the world, only wavelengths, we still have a Theory of Color in optics, because through it we can construct useful artifacts (e.g., a projector that uses the three basic colors, red – green – blue, to create a colorful image on a projection screen); and although ellipses in 3-d are really straight lines in 4-d, the calculations that allow spaceships to navigate around the planets still involve ellipses, three dimensions, and time as a separate dimension, rather than straight lines and four dimensions, because the first option is what we can readily understand.
So, we typically employ the model that’s useful for us in physics, not the one that’s pithier, simpler, more succinct. We do this because we are limited by our human constitution, so we need to work with terms we understand (color, ellipses, and so on). That’s the practical aspect of physics: it helps us build devices, construct things that make our lives easier. But another aspect of physics is that, with it, scientists try to get to the deeper essence of things in the world. Only by trying to understand the deeper essence of nature, for 2,500 years, have people managed to generalize, unify, simplify theories, and eventually gain the necessary insight out of such “grand simplifications” and build useful (and sometimes dreadful) machines. For example, nuclear power (which gave us an alternative source of energy besides hydrocarbons, and — alas! — a Hiroshima and a Nagasaki), became possible only after scientists made the grand unification of electricity and magnetism, which allowed James Clerk Maxwell to come up with the equations for electromagnetic fields, which allowed physicists to gain a better understanding of light and its properties, which allowed Einstein to conceive first of the special, and then of the general theory of relativity, which was necessary for building the devices that harnessed the nuclear power, by converting mass into energy. Even the humble simplification that light is just wavelengths (and therefore that colors are simply a parochial human add-on to the world), was necessary for many of the technological advancements in the 20th century. If we did not have a deeper, generalized knowledge of physics, none of the devices that now surround us — including the internet and the computer on which you read this now — would be possible. We would still be living in candle-lit houses — or maybe huts and shacks — waking and sleeping at the rhythm of our animals.
Thus, physicists keep the complex theories around as long as they prove useful to us; but they also work with the generalizations / unifications / simplifications for two different reasons: (1) to make further advancements in the future, by exploiting the deeper understanding they provide, and (2) because physicists are curious, and want to know how the world really is. What does “how the world really is” mean? Well, if we admit that human beings are an insignificant species that live on a tiny speck of matter that orbits a run-of-the-mill yellow star, which swirls around together with hundreds of billions of other stars in an undistinguished galaxy, one of hundreds of billions of other galaxies in what we call the “universe” (which might also be just one among an untold number of other universes), then we realize that the concept “color” is not really something that should concern physics. It can concern human physics, the kind of physics that results in applications useful for us, but it should not concern the deeper, human-independent understanding of the world. In a similar vein, taking time as something special, separate from space — which is the approach in human physics — gives us all the useful applications today; but it is a human-specific thing, because it is our cognition that makes time appear so special. A human-independent physics should be concerned with 4-d spacetime, at least in the macroworld. And those physicists — or laypeople — who want to know how the world “really is”, should keep the unification of space and time (and, hence, of the unreality of the flow of time) in mind.
But, as I said, aside from all the above, there
is something inherently wrong with my friend’s thought. You can
see what’s wrong in the 3rd objection in the Feedback section (§4), but if you skip there immediately you’ll miss
all the goodies in-between. ![]() Be patient!
Be patient!
2.3 And what about the disappearance of everything?
On that, I have a suggestion to make. It really does not help us in any way to philosophize and conclude that we do not exist. It might be that the space–time unification tells us that our cognition is parochial, and that we are entirely insignificant in the greater cosmic scheme. But then... so what? We already knew that. It’s just that many people refuse to admit it — after all, vanity is part of human nature. But the whole history of science is a story of how human beings learned that they are not special, contrary to appearances. First, they learned that the Earth is not located at the center of the world; then that human beings are nothing special, just another animal species, and that they were not created in some special way, but emerged through biological evolution, just like every other living being; next they learned that there is no universal center at all, and that our location is just as mundane and common as every other location in 3-d space. But in the 20th century, some ideas emerged, mainly among quantum physicists, which implied that human cognition is indeed something special. One such physicist, the British-born American Freeman Dyson, even said, in a way “the universe knew we were coming.” The space–time unification will help us get our senses back, realizing the foolishness of that statement. I think the space–time unification is a good slap on our arrogant faces, letting us wake up and think humbly again. Some might not like this, but the universe cannot care less.
2.4 But what about the illusion of free will?
That’s a problem only if you believe that there is an omniscient being who knows our future (or simply can know it, even if the being does not wish to do so, out of discretion). That is, it’s a problem for some religious people. For me it’s not, because I don’t believe there is anyone who knows my future decisions and actions. If the “now”-slice of my self is as ignorant of my future as I know (and you agree) that it is, then it really does not make any difference whether the actions and decisions of my 4-d self are predetermined or not, since nobody knows them. If you believe that somebody (God?) knows them, then I agree, you are facing a philosophical conundrum. Read further argumentation on this issue in this page of mine.
3. Related Thoughts and Related Work
None of the above ideas is genuinely new, i.e., somebody has discovered some part of it, and stated it in different words; and the list of such people goes back to the ancient times.
| Caveat: Many of the thinkers whose views are presented below concluded that time does not exist. This contradicts the view of the present article, which assumes that time is real, but argues that the flow of time is a cognitive illusion; please read the references below with that in mind. |
-
In the 5th century BC, the Sophist philosopher Antiphon (Ἀντιφῶν) wrote in his On Truth that “Time is not a reality [υπόστασις], but a concept [νόημα], or a measure [μέτρον]”. Parmenides (Παρμενίδης, ca. 500 BC), founder of the Eleatic school, went further, maintaining that time, motion, and change, are illusions. Parmenides’s ideas were best advertised by his student Zeno of Elea (Ζήνων ο Ἐλεάτης, ca. 495 – ca. 430 BC), who posed his famous paradoxes about time, claiming that motion is impossible. The most famous of his paradoxes is the one in which Achilles, the legendary hero and a fast runner, starts 100 m (say) behind a tortoise, who moves at 1/100th of Achilles’s speed. By the time Achilles runs 100 m, the tortoise moves ahead by 1 m; by the time Achilles runs this additional 1 m, the tortoise is ahead by 1 cm; by the time Achilles catches up this extra 1 cm, the tortoise is still ahead by 1/10th of a mm; and so on ad infinitum; therefore, Achilles will never overtake the tortoise. Although today we know where the catch is,(14) Zeno’s paradoxes served to remind to philosophers for centuries that it is by no means obvious that time, motion, and change, must be taken as a priori parts of the ontology of reality.
-
Plato (Πλάτων, ca. 427 – ca. 347 BC) was the first to suggest that we only perceive a distorted view of reality, mere “shadows” of what there really is out there. Plato did this through the “analogy of the cave”, in his Republic, Book VII. In it, Socrates asks Glauco (his interlocutor) to imagine that we are all living in a cave, and are bound in such a way so that we can only look at the wall of the cave, unable to turn our heads. A fire, which we cannot see, is raging from behind and above our heads, projecting the shadows of objects and of ourselves on the cave wall. Having grown up like this since our childhood, we take the shadows to be the objects themselves. But now suppose someone unlocks and loosens our shackles, and leads us out of the cave, to the sunlight. Then we would feel that our eyes hurt, due to the sudden brightness, and we would take quite some time to get accustomed to seeing not just shadows anymore, but the objects in and of themselves.
Plato, being an idealist (as opposed to being a materialist), used the analogy of the cave to argue that beyond the world of immediate material experience there is the world of pure and perfect ideas, the imperfect shadows of which we usually are bound to observe in our lives. But he came so tantalizingly close to the idea that the material world is the one which is different and we only perceive distorted shadows of it, that I think he deserves the title of the first thinker who saw the limits of human cognition, thus leaping thousands of years ahead of his time. (Whether Socrates himself really discussed the analogy of the cave with anyone is a moot subject; Plato usually employed his teacher, Socrates, as a character in his dialogues, to argue for or against some philosophical point.)
-
Gottfried Wilhelm von Leibniz (1646 – 1716) was the first philosopher after the Greeks to propose that time does not exist, that it is an illusion of the human intellect. Similar views were held by Immanuel Kant (1724 – 1804). However, the view of time discussed in the present text cannot be called “Leibnizian”, because Leibniz believed that time and space are not real but part of a conceptual apparatus (along with Number — e.g., see here), thus rediscovering the ideas of ancient Antiphon (see above). Leibniz believed that the mind creates and gives substance to time and space. In contrast, the present view assumes space and time are real, but the latter is much more similar to the former than our cognition makes us believe; contrary to Leibniz, here space and time are assumed to be entities independent of the human mind, and it is only the flow of time which is claimed to be a cognitive illusion.
-
James B. Hartle’s textbook Gravity (see it in Amazon) was the main source I used as reference in order to verify most of the ideas discussed here. It is a wonderful text that shows how 4-d space-time physics can be seen simply as the geometry of 4-d curved space. Converting physics to geometry is at the heart of the present discussion, and Hartle’s book does an excellent job to that end.
-
Julian Barbour wrote the book The End of Time: The Next Revolution in Physics, in 1999 (see it in Amazon). To tell you the truth, I tried to read this book but couldn’t. Beyond the introductory chapters I found it too technical, and beyond my grasp. I read in Amazon that others express similar concerns, but one reader makes the following interesting comments:
“Basically, what Julian Barbour does, is nothing less than a total reconstruction of the whole of physics, based on the Leibniz vision of time. He first shows how classical physics can then be understood. Then he moves on to do the same with the special and general theories of relativity of Einstein. After having done that, he even moves on to quantum mechanics. Does he succeed? I think he does. [...]
The only objection about Julian Barbour’s approach is, essentially, the same you can rise against the Leibniz view of time as such. Philosophically speaking, if you begin by assuming that there is no real change, and that all change is ‘illusion’, only ‘existing in the mind’, then you have to explain how this ‘illusion’ can arise, without introducing movement ANYWHERE. All such attempts have failed.”
I don’t think Barbour’s view is Leibnizian (the above reader does not say so), but the reader’s concern about how the illusion can arise without introducing movement anywhere is answered easily by the LP-musical-disk analogy (discussed earlier in the text): the music (corresponding to cognition, or thoughts), is a notion of the time-sliced perception only; when one looks at the LP as a whole, music vanishes, it is nowhere to be perceived. Thus, that “the flow of time is an illusion” means that when we consider time-slices, we get cognition and its accompanying illusion of the temporal flow; but when we consider spacetime as a whole, there is no illusion. The above reader wants to find the illusion in the 4-d holistic view, where there is none to be found. The illusion arises only when we introduce movement, which happens in the 3-d time-sliced point of view.
My understanding is that Barbour’s book explains the details of the physics of the present view, without going into the philosophical implications, which, however, I find much more important. (We do have a very successful model of spacetime in physics, after all, one that does not seem to be in need of repair at present.)
Now I must confess one thing: I wrote the rest of this section halfheartedly only. The reason is that the literature that helped me crystallize the above thoughts is the one I already referenced in §2, plus a large number of other books that contributed to my general knowledge. But if I don’t mention the work below, people will bring it to my attention: “Oh, but haven’t you read such-and-such’s writings?” I might have read them (or read reviews of them), but they didn’t really contribute anything, for the above ideas to develop — at least that’s how it appears to me. In any case, I’ll do my preemptive strike, listing the work that I am aware of (some of it tangentially only related):
-
John Ellis McTaggart wrote The Unreality of Time in 1908 (published in Mind: A Quarterly Review of Psychology and Philosophy 17 [1908]: 456–473). (Read it here.) In it, McTaggart introduced the terminology of “A series” and “B series”, where by “A series” he meant the sequence of events as we perceive them from our point of view (from “inside”, so to speak), which includes a “now”, and by “B series” he meant the holistic view of sequences of events, where there is no privileged “now”, but in which we can compare events chronologically and say this event is before that one, and so on. McTaggart proceeds in his paper to first show that the A series is more fundamental than the B series for the description of time, and then to show that no A series can exist, thus concluding the unreality of time. He shows — or thinks that he shows, anyway — that no A series can exist by observing that each event must be assigned three mutually incompatible labels: every event is initially in the future, later it becomes present, and finally is relegated to the past. McTaggart thinks that we cannot ascribe three incompatible labels to a single event, hence no A series can exist.
But this sounds to me as mere sophistry. Why should only one temporal label be assigned to each event? Why are the labels “past”, “present”, and “future” mutually incompatible? They are compatible if we assign each at a different time. McTaggart thinks that we cannot do so, because our purpose was to explain time in the first place, so we cannot use time to make the labels compatible, or we end up with a vicious circle. But we don’t have to explain time; we can take it as fundamental. McTaggart does not want to accept time as fundamental, he wants to explain it, and that’s why he falls into the logical abyss. He reasons like this: “Anything defined in terms of simpler notions is not fundamental; I want to define time in terms of simpler notions; but I cannot; therefore, [instead of concluding that time is fundamental] time is unreal!” Does his reasoning make any sense? I think not, because it implies that anything fundamental — hence undefined — must be unreal! Today we know we can consider time as fundamental and devise a logic with which we can talk consistently about temporal events through the various “temporal logics”, which are cases of modal logic. I don’t blame McTaggart for not knowing this back in 1908, but I cannot understand the insistence of some present-day philosophers in referencing McTaggart’s paper as an essential contribution on the subject of time.
-
D. H. Mellor’s book, Real Time II (1998, Routlege; here it is in Amazon). Well, what I can say about this book is that... I’ve read it. Yup! Now, if you ask me what do I remember of it, I’d have to stare at you expressionless for awhile, digging deep in my memory... I recall reading about the asymmetry of time, its directionality, and its isotropy/anisotropy question. But I had read about these notions elsewhere. Oh, yea, Mellor takes McTaggart seriously. OK, I better stop. Read the book if you are interested in a serious philosopher’s essay on the serious subject of time.
-
Palle Yourgrau’s book, A World Without Time: The Forgotten Legacy of Gödel and Einstein (2005, Basic Books; in Amazon). I find this book tangential to the subject only (in spite of its catchy title, which was what made me rush to buy it). Read pp. 128 – 131, titled “Gödel’s Dialectical Dance with Time”, to understand what the gist of the book is. In those pages, Yourgrau says:
“The equations of general relativity permit alternative solutions, each of which determines a possible universe, a relativistically possible world. Solutions to these complex equations are rare, but in no time at all Gödel discovers a relativistically possible universe (actually, a set of them) — now known as the Gödel universe — in which the geometry of the world is so extreme that it contains space-time paths unthinkable in more familiar universes like our own. In one such Gödel universe, it is provable that there exist closed timelike curves such that if you travel fast enough, you can, though always heading toward your local future, arrive in the past. These closed loops or circular paths have a more familiar name: time travel. But if it is possible in such worlds, Gödel argues, to return to one’s past, then what was past never passed at all. But a time that never truly passes cannot pass for real, intuitive time. The reality of time travel in the Gödel universe signals the unreality of time. Once again, time disappears.
But the dance is not over. For the Gödel universe, after all, is not the actual world, only a possible one. Can we really infer the nonexistence of time in this world from its absence from a merely possible universe? In a word, yes. Or so Gödel argues. Here he makes his final, his most subtle and elusive step, the one from the possible to the actual. [Gödel’s argument is that] if a mathematical object is so much as possible, it is necessary, hence actual. This is so because what necessarily exists cannot exist at all unless it exists in all possible worlds. [...]”
Does this last “argument” ring any bell? How about this one: “Ontological argument for the existence of God”? Yes, right? “If God is so much as possible, He is actual” (Yourgrau mentions this next, verbatim). This is the most ridiculously idealistic, I-want-it-to-be-true-no-matter-how-dumb-it-sounds argument I have ever heard. Even Plato, the Grand Idealist, didn’t dare to utter such absurdities. So, if Beings with legs sprouting out of their nostrils and marijuana leaves hanging from their nipples are so much as possible, They are actual. Right. Further, we read:
“In the case of the Gödel universe, he reasoned that since this possible world is governed by the same physical laws that obtain in the actual world — differing from our world only in the large-scale distribution of matter and motion — it cannot be that whereas time fails to exist in that possible world, it is present in our own. To deny this, Gödel reasoned, would be to assert that ‘whether or not an objective lapse of time exists (i.e., whether or not a time in the ordinary sense exists) depends on the particular way in which matter and its motion are arranged in this world.’ Even though this would not lead to an outright contradiction, he argued, ‘nevertheless, a philosophical view leading to such consequences can hardly be considered as satisfactory.’ But it is provable that time fails to exist in the Gödel universe. It cannot, therefore, exist in our own. The final step is taken; the curtain comes down: time really does disappear.”
If you manage not to be distracted by Yourgrau’s melodramatic and theatrical closing lines, you’ll see that he is trying to make some point there. But does time really disappear in Gödel universes? Why does time disappear if there are closed loops in those universes? This was not entirely clear to me after reading Yourgrau’s book. Further, why if something does not exist in a Gödel universe then it cannot exist in our own? If elephants cannot exist in a Gödel universe, does it follow that our universe must not have elephants either? What kind of illogical logic is this?
-
George F R Ellis’s paper, Physics in the Real Universe: Time and Spacetime (read it here, in pdf). Ellis’s paper makes a false assumption: that, supposedly, the idea of a block universe “is based on time-reversible microphysical laws, which fail to capture essential features of the time-irreversible macro-physical behaviour and the development of emergent complex systems, including life, which exist in the real universe”, as we read in the Abstract. But the block-universe view does not restrict itself to the time-reversible laws of classical and relativistic physics; it encompasses every nook and every cranny of the universe, including life (and, as I toiled to explain, cognition). The world, biology and all, simply is. Its temporal irreversibility is included. My understanding is that Ellis sets up and attacks a straw man argument.
-
Paul Davies’s classic About Time: Einstein’s Unfinished Revolution (1995, Simon & Schuster; in Amazon). Best explanation of the relativistic Twin Paradox; other than that, well... Davies writes in an easy to read, entertaining way. Introductory in relativity, too.
-
Stephen Hawking’s classic, A Brief History of Time (1996, Bantam Books; in Amazon). Introductory, and elementary. Read it only if this is one of your firsts on the subject, or if you enjoy classics. (I put it in this list only because the world is large, the web worldwide, and somebody is going to recommend it to me if I don’t.)
4. Feedback
How much of the above is true? I am interested
in receiving feedback. But before contacting me to complain that you don’t feel you have disappeared
at all, please make sure you have understood the contents of this
page adequately enough, perhaps having some insight that eluded
me. If you think that this is the case, I’ll be more than happy
to learn why you still exist. ![]() However, this page is not a blog, so I will not
include here every random opinion, but only those that, in my
judgment, are possible objections to the disappearance act. I
will present such opinions anonymously only.
However, this page is not a blog, so I will not
include here every random opinion, but only those that, in my
judgment, are possible objections to the disappearance act. I
will present such opinions anonymously only.
![]() 1.
A reviewer, a professor of physics (I think), brought up the
following objection: “[T]his ‘argument’ does not have
anything uniquely pertinent to special relativity as compared to
any other theory.” What the professor meant is that the same
arguments as the ones expounded above could also be used without
reference to Einstein’s relativity. For example, I could be
using a 4-D Galilean space, i.e., a space with Euclidean
geometry, and the arguments would be identical. Relativity is
irrelevant, the professor said.
1.
A reviewer, a professor of physics (I think), brought up the
following objection: “[T]his ‘argument’ does not have
anything uniquely pertinent to special relativity as compared to
any other theory.” What the professor meant is that the same
arguments as the ones expounded above could also be used without
reference to Einstein’s relativity. For example, I could be
using a 4-D Galilean space, i.e., a space with Euclidean
geometry, and the arguments would be identical. Relativity is
irrelevant, the professor said.
I don’t think so. A 4-D Galilean physics, i.e., one based on Euclidean geometry, does not explain why we perceive one of the dimensions (which we call “time”) as special. Why that dimension appears different? Why one of the four? Indeed, the metric in Euclidean 4-D space is given by the formula: d2 = x2 + y2 + z2 + t2, where x, y, and z stand for the three spatial dimensions, and t for the temporal one. But all four dimensions show a complete symmetry in this formula. We can freely interchange t with any of the x, y, z in this formula, and nothing will change; for example, we can write d2 = x2 + t2 + z2 + y2, and christen “spatial” the dimensions x, t, and z, and “temporal” the dimension y. In contrast, in 4-D Minkowskian geometry, the metric is: d2 = x2 + y2 + z2 – t2, which tells us very explicitly that one of the four dimensions differs from the other three: it is the dimension that has the minus sign in the formula of the metric; that is the dimension we perceive as “time”, and to which we ascribe temporal properties. Why? because if we summarize x2 + y2 + z2 by s2 (i.e., if s is our familiar 3-D spatial length), then we get d2 = s2 – t2. Now if we set d = 0, which means that we are interested in finding out which spatio-temporal coordinates result in simultaneous 4-D events (see also the discussion in §1.6), then we obtain |s| = |t|, or: the length of space equals the length of time for such events. This is possible only in the Minkowskian geometry of special relativity.
Also, relativity is relevant in another important way in the above disappearance act: It is because of the relativistic relation of mass and energy that one can conceive of “plasmoids”, placing them close to the opposite end of the mass–energy range from the one we occupy: i.e., the plasmoids have mostly kinetic energy but not much inertial mass, whereas we have mostly inertial mass but not much kinetic energy. None of the above arguments would hold if relativity were missing from the picture.
![]() 2.
The same reviewer objected by arguing that Minkowskian geometry describes a
spacetime devoid of mass and energy, and spent about two full pages to tell me
(in various rephrasings and word-permutations of the same idea) that general
relativity does away with Minkowski spacetime, and instead employs Friedman
spacetime, in which we live, since there is not just empty spacetime, but also
mass and energy in our world. Thus, since I do not make reference to Friedman
spacetime and general relativity, the professor thought, my arguments are
irrelevant in the real world. Specifically the professor wrote:
2.
The same reviewer objected by arguing that Minkowskian geometry describes a
spacetime devoid of mass and energy, and spent about two full pages to tell me
(in various rephrasings and word-permutations of the same idea) that general
relativity does away with Minkowski spacetime, and instead employs Friedman
spacetime, in which we live, since there is not just empty spacetime, but also
mass and energy in our world. Thus, since I do not make reference to Friedman
spacetime and general relativity, the professor thought, my arguments are
irrelevant in the real world. Specifically the professor wrote:
“The most basic misunderstanding of Einstein’s relativity theory underlying this article is that the author does not seem to know that Minkowski spacetime is the vacuum solution to the field equations of the general theory of relativity, implying that Minkowski spacetime cannot contain matter, observers and the like. But the author’s article is about a Minkowski spacetime that is posited as containing matter, motion, observers, etc., and the author is attempting to derive conclusions about space and time from this self-contradictory assumption (viz., that there is matter, motion, observers, etc. in a universe whose metric, line element and symmetry group [the Poincare group] precludes the presence of matter, motion, observers, etc.”
Fine. (Well, not fine: I am not just an “author”
to be reviewed, dear professor, but the great magician Harry
Foudini, as I already announced in the preface; and you will
disappear, nonetheless, for all your laudable efforts.
![]() ) However,
the professor missed a tiny yet crucial detail: nothing in this article requires
that space-time be flat, thus described by the Minkowskian geometry of special
relativity, and not curved, thus described by Friedman space-time. Let’s be more
specific and explicit:
) However,
the professor missed a tiny yet crucial detail: nothing in this article requires
that space-time be flat, thus described by the Minkowskian geometry of special
relativity, and not curved, thus described by Friedman space-time. Let’s be more
specific and explicit:
-
Special relativity can be seen as the geometry of flat 4D space-time.
-
General relativity can be seen as the geometry of curved 4D space-time; where, of course, what curves space-time is the presence of mass–energy.
Now, the basic observation that led to this article is not that 4D space-time is flat, but that time is another dimension on par with the three dimensions of space; i.e., that space and time are the same “stuff”; i.e., that s = t; and this holds whether space-time is flat or curved; it holds both in special and in general relativity. Thus, the professor’s remark that Minkowskian geometry (flat space-time) is a prerequisite for reaching the conclusions that we reached is simply not true.
Still, however, there is something worth pondering about, implied by the professor’s objection: if space-time is curved due to the presence of mass, why do we use the Minkowskian geometry of flat space-time to reason at all about observers, who have mass? Why not using general relativity and Friedman space-time, and thus avoid objections such as the above?
Because even though generally space-time is curved (and thus general relativity applies), locally the curved space-time is flat (barring singularities, such as black holes). This follows from the “equivalence principle” (e.g., see Hartle, §6.3), which says that the results of experiments that are done in sufficiently small space and that last for sufficiently short time cannot be distinguished from the results of the same experiments done in an inertial frame. Mathematically, this means that the space-time which is curved due to the existence of mass is smooth and continuous, and everywhere differentiable (again, excluding singularities). Thus, if we have a general metric gαβ(x) in some system of coordinates (I’m following Hartle’s notation, see his §7.4), then it is possible that for every point (or “event”) P of space-time we can define new coordinates x΄, such that: g΄αβ(x΄P) = diag(–1,1,1,1), which is the Minkowskian metric of flat space-time. This requirement is one of the assumptions of general relativity, and implies that at every point P there are three spatial coordinates and one temporal, whether mass exists at P or not. But what does all that mean practically, for us observers?
It means that we human observers, with the negligible masses of our environment, live in a world that’s a special case of the general one. We don’t walk on the surface of a neutron star, nor do we navigate in the vicinity of a black hole. Our world is essentially flat, devoid of mass and energy, at least of the amount of mass–energy that would make space-time truly (perceptibly) curved, and Friedman’s generalized solution relevant and indispensable in human cognition. Thus, given the parameters of the world in which we evolved, Minkowski space-time is still the space-time of our environment to an excellent approximation (although, as discussed earlier, we perceive it as an even simpler one: as Euclidean 3-d space + time). The vacuum solution to the field equations of general relativity is precisely what gives rise to our cognition; and it is the reason why Einstein arrived first at special relativity with its Minkowskian space-time: because that’s what we get under the assumption that there isn’t much mass around, and thus that space-time is locally not curved. General relativity might be “more correct” than the special one, but it is not particularly helpful in explaining our perceptual and other cognitive properties. In a sense, general relativity is an overkill for cognition, “too much” for us, tiny human observers — in a way reminiscent of the one in which quantum mechanics is too remote from our ordinary experience (read this article of mine on that subject).
The bottom line is: Minkowskian geometry is used in this text to explain not the universe itself, but our cognition, our perception of the universe and its properties; to explain not time itself, but our perception of time.
![]() 3. Another reader’s
objection was based on more philosophical grounds. The reader
thought: so what if it is possible to unify time and space,
eliminating the temporal properties of time; that it is possible
does not imply that it has to be thus. I might have
shown that the flow of time can possibly be a
cognitive illusion, but this does not make it an
illusion. It could still be the case, according to that reader’s
opinion, that the flow of time is real (i.e., we are 3-d spatial
beings who are presented with events of the future, time-slice
after time-slice), and that the cognitive illusion suggested in
this text is a mere curiosity: a possibility, but not the
reality.
3. Another reader’s
objection was based on more philosophical grounds. The reader
thought: so what if it is possible to unify time and space,
eliminating the temporal properties of time; that it is possible
does not imply that it has to be thus. I might have
shown that the flow of time can possibly be a
cognitive illusion, but this does not make it an
illusion. It could still be the case, according to that reader’s
opinion, that the flow of time is real (i.e., we are 3-d spatial
beings who are presented with events of the future, time-slice
after time-slice), and that the cognitive illusion suggested in
this text is a mere curiosity: a possibility, but not the
reality.
Originally (up to Oct. 2007), I had given an answer for the above objection in this page. My answer was based on the notion that the idea of time-flow-as-cognitive-illusion makes more sense from the point of view of philosophy and physics, because it results in a simplification (it gets rid of notions such as time-flow, past, present, future, etc.), and that the more complex (but, alas, so familiar!) alternative should be rejected by appeal to Occam’s razor. (I even referred the reader to a justification for Occam’s razor, see below.) But later another reader agreed with the first one — in spite of my answer — telling me that, yes, a possibility does not make a certainty. So I thought, wait a minute, can this be a matter of personal preference? Can someone say, “I prefer this because it chimes better with my intuition!”? There must be some objective way to decide which view is real.
Upon further consideration I believe I found an inherent flaw in the above reader’s view. Now, I’ll explain what the flaw is immediately, but I don’t want to trash completely my earlier reply, because there were some interesting (to others, I hope, not just to me) comments there. So I’ll proceed with my newer reply first, and after that I’ll enclose my earlier reply in a box (find it further below), for the interested reader to look at. (A link to a justification for Occam’s razor is given there.)
So: according to that reader’s objection, it could be that we are 3-d beings who are presented with events, time-slice after time-slice. Yea, why not?
Not, because this works in a Euclidean, wrong view of spacetime. Spacetime is relativistic, and this has been shown with countless experiments. I’ll explain.
Let’s first see what a Euclidean “time-slice after time-slice” view of reality means. It means that now our 3-d world looks like this; the next moment, our 3-d world looks like that; then, a moment after that, it has yet a different configuration; and so on. Normally I should draw these 3-d slices by placing them next to each other, and assume that time presents them to us from left to right, one after the other. But because it is impossible to draw 3-d chunks of space next to each other, what authors usually do to illustrate this idea is to reduce the dimensions of our space from 3 to 2; so imagine that ours is a 2-d spatial universe, looking like a flat sheet of paper. Now we can stack such 2-d slices next to each other, as Figure 4.1 shows, imagining that each slice is our whole universe, and is presented to us at a given time t1; the next moment, t2, the slice following it is presented; and so on.
Figure 4.1: View of the world as it appears to those who raise the present objection
But, as I mentioned above, the view of the world as shown in Figure 4.1 is wrong. Here is why: suppose you are standing somewhere, and a friend of yours is moving with a constant speed relative to you (Figure 4.2). Then your friend is perceiving different time-slices of the world than those that you perceive. Before Einstein, with the physics of Newton and the geometry of Euclid, people thought that everybody perceives the same time-slices, as in Figure 4.1. But after Einstein, with relativity, we learned that the situation in reality is different: you and your moving friend perceive time-slices as shown in Figure 4.2.
Figure 4.2: Slices are different if observers move relative to each other
The time-slices of the universe that you and your friend perceive are drawn at a relative angle a in the figure, and this angle is correlated with your relative speed (not exactly proportionally; but for the figure to make good sense we can say that as your relative speed approaches c the angle a approaches 90°).
So if the universe is “served” slice after slice, it is obviously served differently to each moving observer.
It gets more complicated than this, but let’s stop for a minute and ponder: if you feel that the “now” is one of those time-slices, which part of yourself perceives that now-slice? If you move your arm relative to your head, won’t your moving arm be in a different time-slice than your head? And where is the “you” that experiences the slice, the “now”? Are “you” in your head, excluding your moving arm? Are “you” at a point inside your brain? Any neurologist or cognitive scientist will tell you that there is no such point in your brain where the “I” resides; all information in the brain is distributed. The idea that the “I” occupies a specific point in space is unscientific, baseless. So you cannot identify the “now” that “you” just experienced with a particular time-slice of the universe, because if you take any time-slice you don’t know where to position the “you” with respect to that slice.
But, as I said, it gets more complicated than that. Figure 4.2 concerns observers moving relative to each other with constant speed. But in reality observers move by accelerating and decelerating. When you de-/accelerate, the time-slices of Figure 4.2 will acquire local dents. Your friend’s slices would have dents, too, and so would all the slices of all the billions of people on Earth, so the slices would mix and intermingle with each other. Further, the farther moving observers are from each other in space, the more their slices differ (see Greene,[1] pp. 132–139). If there are observers in the Andromeda Galaxy (or if your descendants travel there one day in the distant future), they would get completely different slices from you. Who, or what mechanism “serves” all those slices to all those observers? And who qualifies as an observer in the first place? Do all the billions of people on Earth count as observers to be served with slices? Don’t animals count? Isn’t your pet an observer? A baby? When does a baby become an observer? Starting as a one-cell creature, I suppose you’d agree that that is not an observer — it’s a potential one, but a single-celled creature does not observe anything yet — lest you are willing to admit this for every cell of your body. So when, at which magic moment does a baby acquire the status of an observer? Apparently there is no such magic moment, which means that the notion of “observer” cannot be defined in a sensible way; and this means that the notion that the universe is served slice-after-slice to observers cannot make much sense either.
OK, the above is my newer reply, and hopefully the final one. However, my earlier reply is shown in the box, below:
| I repeat, this is my earlier reply to the above
objection; a reply that I now consider insufficient, but
still including some hopefully interesting points: I suppose it could be as the reader suggested (and as virtually every person in this world intuitively feels is the case). I cannot prove that an illusion is going on. I can only suggest that (unfortunately) the idea of a cognitive illusion makes more physical sense, in the same way that the idea that the Earth and other planets orbit the Sun makes more physical sense than the idea that the Earth is immobile and all other planets, including the Sun, rotate around it on the celestial sphere (or spheres) in the course of a 24-hour period. The latter idea is a cognitive illusion; the former is reality. However, there are reasons for which the analogy I just brought up breaks down: we can perform a number of experiments and verify whether the Earth rotates around the Sun or whether the Sun (and everything else) rotates around the Earth. For example, if the Earth rotates around the Sun in the course of one year (as indeed it does), then we must be experiencing an extremely weak “centrifugal” force with a direction perpendicular to the tangent to the Earth’s orbit, away from the Sun, and this force must be measurable with some extremely sensitive instrument. Alternatively, we can conclude the correctness of the Copernican system (and the demise of the Ptolemaic one) with a simple thought: if the Earth is immobile and the planets rotate around the Earth in the course of a 24-hour period, then it turns out (as we can find out after a few simple calculations) that the planet Neptune — and everything that stands at a greater distance — must be rotating around Earth at a speed greater than the speed of light (a “superluminal” speed); but no object with mass greater than zero can move at a superluminal speed; therefore, by making use of modern knowledge, we can conclude with an armchair argument that the Ptolemaic system does not hold any water. Fine; so, could there be some experiment, or even thought experiment, that could tell the cognitive illusion idea and the “intuitive physics” (3d-space + 1d-time) apart? There might be, but at present I am not aware of any. A good reason that I have for suggesting that the cognitive illusion idea is the correct one is an appeal to the continuation of economy in physics. By this, I mean the following: even if there were no experiments (real or of thought) to make to tell the Copernican and Ptolemaic systems apart, still the former would be preferable because it is more economical than the latter: it describes nature in fewer and simpler terms. Our preference for the Copernican system is a typical application of Occam’s (or Ockham’s) razor: “Entities should not be multiplied needlessly”. The introduction of countless spheres-within-spheres and the complexity of the epicycles that the Ptolemaic system requires are cut off by Occam’s razor and replaced by the simpler Copernican (actually Keplerian) ellipses. Now, the cognitive illusion idea does not make such a dramatic reduction in complexity compared to the “intuitive physics”, I admit that much. But it causes some simplifications, nonetheless. Specifically, the intuitive physics uses two qualitatively different notions: space and time (note that even though general relativistic physics treats space and time as one idea, spacetime, what I mean by “intuitive physics” is the way time is presented in college physics textbooks: as an entity distinct from space), whereas the cognitive illusion idea does away with the need to talk about time as separate from space. Essentially the cognitive illusion explains why relativity deals with a unified spacetime and not with 3d-space + 1d-time; it also explains why time appears symmetric in physics formulas (Greene’s puzzlement): because it is locally symmetric, and it is only our cognition which gives us the illusion that time “flows” in one direction. (Why it is the direction we perceive and not the opposite one is the subject of this page.) There is at least one more sense in which the cognitive illusion idea is more economical than intuitive physics: the latter, with its “flow” of time, implies some kind of “speed” by which the time “flows” (a topic discussed earlier), and one is left wondering, why time is sensed as flowing at this particular “speed” and not some other one? Why is its “speed” sensed as uniform, why does it not sometimes speed up, and other times slow down? The cognitive illusion tells us that there is no such thing as flow and speed of the passage of time; we experience the smoothness of the flow perhaps because of the way our cognition keeps track of time — in any case, the smoothness of the perceived flow is an issue out of the domain of physics, and probably one in the domain of cognitive science in want of an explanation. So: would you prefer one idea over another solely on the basis of Occam’s razor? The reader who brought up this objection did not think that Occam’s razor constitutes a sufficient basis. But I think it does, because Occam’s razor is not just an intellectual tool, good for philosophical discussions only, but a fundamental pillar of cognition, as I explain in this article (see the “2nd principle” in that article): a “law” that we use every moment, unknowingly, throughout our lives. In addition, Occam’s razor has worked wonders throughout the enterprise of physics; there is no reason to throw it now out the window because we are sentimentally attached to a more intuitive — even if more complex — view of the world. Back in the times of Copernicus, I imagine there were thinkers who objected to the idea that the Earth is not at the center of the world, based on purely sentimental reasons. The cognitive illusion idea similarly attacks a cherished belief: that cognition is something special in the universe (recall Freeman Dyson’s thought). But our liking or disliking should not be a reason for selecting among explanatory alternatives. |
That’s what I have in terms of feedback, so
far. Feel free to contact me and
add to this discussion, supporting your existence in some way
that I overlooked. ![]()
Footnotes (clicking on the footnote number you move back to the text):
(1) Notice that every surface is mathematically an object of two dimensions, even though it might be curved in 3-d space. This is because locally (in the vicinity of any point) every smooth surface resembles a flat plane, which is 2-dimensional. Even a surface with edges can be approximated by a collection of intersecting planes.
(2) I put the prefix macro- in front of “dimensions” because some quantum physics theories, including string theory, postulate the existence of a number of additional microdimensions. This fact will not concern us, however, because here we examine the large-scale structure of the world.
(3) The truth is there are some physical systems that break the time symmetry, but they are rather not very important. In particular, there are some relatively esoteric particles, such as K-mesons and B-mesons, that show the so-called weak nuclear force does not treat past and future fully symmetrically. However, Greene, along with other physicists, thinks that since these particles play essentially no role in determining the properties of everyday material objects, they are unlikely to be important in explaining the puzzle of time’s psychological asymmetry (Greene, 2004,[1] p. 495).
(4) Let us clarify these two terms: the asymmetry of time refers to the observation that the past seems different from the future (and the future different from the past). The directionality of time refers to the feeling that our lives seem to be moving from the past and into the future. If the reader has difficulty distinguishing between the two notions, maybe an analogy will help: think of a cone; the cone is asymmetric along the direction that runs its length, because it is narrower at its tip, and thicker at its base. But we cannot assign any particular direction to this asymmetry, because we may run the length of the cone either starting from the tip and ending at the base, or starting from the base and ending at the tip. If we do decide to choose one particular direction among the two, say, from the tip to the base, then we have given directionality to the asymmetry of the cone. Similarly, we experience directionality in time when we feel the future coming toward us, and the past being left behind, and not the other way around.
(5) It is reminiscent of the Moon illusion: whenever you measure the Moon’s apparent diameter with physical instruments you find the same value. But whenever you look at it, it appears very different depending on whether the Moon is close to the horizon (larger), or to the zenith of the sky (smaller).
(6) The term “plasmoid” exists in modern physics, but it has a very technical meaning. It means, “tailward fast plasma flows with dipolar Bz signatures […] observed within plasma sheet” (in Hones, E. W., Jr., D. N. Baker et al., 1984: “Structure of the magnetotail at 220 Re”. Geophys. Res. Lett., no. 11, pp. 5-7). So there is no risk of confusion with our usage of the term here, since we use it in a different, non-technical context, although the meaning of the root word (“plasma”) is kept intact. The meaning of the suffix “-oid” should be understood by analogy to the meaning of the same suffix in words such as “humanoid”, etc.
(7) For another example, just because it is physically possible for an object to move in space faster than a bullet, does not mean that some species of animals must have evolved that can achieve this.
(8) c is large objectively, not just to us, measuring it in a certain unit of space over a certain unit of time: of all relative speeds that are possible for massive objects, c is the largest value, and zero the smallest.
(9) A physicist-reviewer of an earlier draft of this article showed some difficulty to accept this idea, thinking that it violates the relativistic result that no object with non-zero mass can attain the speed of light (let alone exceed it). Perhaps this person did not possess the necessary patience to understand this simple point. The idea is that the sum of inertial mass and kinetic energy of the object remains constant, and what varies is the percent of mass over the total [mass+energy]. If we zero the mass, the energy will reach a maximum value, and if m0 was the original inertial mass of the object, then the maximum energy E will be equal to m0·c2. At that point, the object will have mass m = 0, and energy E, moving at speed c. What is required to imagine is a mechanism for the conversion of mass to energy (a mechanism that the mitochondria in our cells already possess). There does not seem to be any violation of relativity. Now, one might claim that a total conversion of m0 to E is not physically possible (because the mechanism itself would be destroyed in the process of conversion), therefore the plasmoids cannot exist in reality (which is an argument distinct from the charge of violation of relativity). But recall that plasmoids are hypothetical beings, imagined for the purposes of a thought experiment; their non-existence in reality (and the unrealizability of their exotic properties) neither weakens nor enhances this argument. In other words, I agree that plasmoids do not, and cannot, exist in reality; but this is entirely irrelevant for the purposes of a thought experiment that is invented to help us understand some features of our own, human cognition.
(10) Plasmoid physicists would not measure velocity v = s / t, but its inverse v-1 = t / s, because s / t may yield division by zero in the case where t remains fixed and there is motion in space (what to us would appear as motion at speed c). Assuming division by zero causes to plasmoids the same aversion as it does to us, v-1 would be a more meaningful quantity in plasmoid physics. The larger v-1 is, the more the plasmoid energy is “impeded” from moving at its natural speed, c.
(11) Note that a plasmoid’s energy does not reach infinity. Here we are not talking about objects with a fixed mass that reach the speed of light (in which case their energy becomes infinite), but about creatures that can regulate the amount of mass they possess, so that their total amount of mass + energy remains constant.
(12) The reader might think that such an idea is meaningless, because in ordinary experience “motion” implies change that happens in time. But it must be noted that in the present a generalized concept of “motion” is used, by which is meant nothing more than a sequence of space-time coordinates, constituting either a discrete, or a continuous set. The immediately following paragraph explains this notion further.
(13) Heraclitus ( Ἡράκλειτος ) was a Greek philosopher who lived around 500 BC, in the town of Ephessus ( Ἔφεσος) in Asia Minor (present-day Turkey). Heraclitus’s famous dictum was “Everything flows, and nothing stays” (Τὰ πάντα ῥεῖ, καὶ οὐθὲν μένει).
(14) The catch is, as we learned in the mathematics of
infinite series (which was unknown in Zeno’s time), that the
sum of an infinite sequence of numbers can be a finite number.
Thus, although the space that both Achilles and the tortoise run
is divided into an infinite sequence of intervals, if we sum up
those intervals we end up with a finite total length, therefore
Achilles will meet the tortoise within a finite time (and will
subsequently overtake it).
The layperson sometimes still objects to this explanation by
arguing as follows: suppose Achilles reaches the first landmark
of 100 m in 10 seconds, so we take a snapshot (a picture) at that
moment; at the next landmark, at 101 m, we take another snapshot,
i.e., at 10.01 s; the next snapshot is taken at 10.0101 s, and so
on ad infinitum; but since we will always be able to
take snapshots, our snapshot-taking session will never end.
This reasoning, although mathematically makes some sense, is at
fault on two physical counts. First, it is not true that
we should always be able to take snapshots, i.e., pictures,
because as the time-intervals become shorter and shorter, at some
time it will become impossible for light to traverse the distance
between the runner and our camera, so no picture will be taken
beyond that point. And second, there is the problem that this
idea assumes time is infinitely divisible, which might not be
true (time might be discrete).
References (clicking on the reference number brings you back to the text where the reference is first made):
[1] Greene, Brian R. (2004). The fabric of the cosmos: space, time, and the texture of reality. New York: Knopf.
[2] Einstein, Albert. (1905). “On the electrodynamics of moving bodies”. Annalen der Physik, vol. 17, pp. 891-921.
[3] Dickson, W. Michael (1998). Quantum Chance and Non-Locality: Cambridge University Press.
Back to Harry’s index of topics in philosophy