
SEHR, volume 4, issue 2: Constructions of
the Mind
Updated July 22, 1995
Douglas R. Hofstadter
Because it began life essentially as a branch of the theory of
computation, and because the latter began life essentially as a
branch of logic, the discipline of artificial intelligence (AI)
has very deep historical roots in logic. The English logician
George Boole, in the 1850s, was among the first to formulate the
idea--in his famous book The Laws of Thought--that
thinking itself follows clear patterns, even laws, and that these
laws could be mathematized. For this reason, I like to refer to
this law-bound vision of the activities of the human mind as the
"Boolean Dream."1
Put more concretely, the Boolean Dream amounts to seeing thinking as the manipulation of propositions, under the constraint that the rules should always lead from true statements to other true statements. Note that this vision of thought places full sentences at center stage. A tacit assumption is thus that the components of sentences--individual words, or the concepts lying beneath them--are not deeply problematical aspects of intelligence, but rather that the mystery of thought is how these small, elemental, "trivial" items work together in large, complex (and perforce nontrivial) structures.
To make this more concrete, let me take a few examples from mathematics, a domain that AI researchers typically focused on in the early days. A concept like "5" or "prime number" or "definite integral" would be thought of as trivial or quasi-trivial, in the sense that they are mere definitions. They would be seen as posing no challenge to a computer model of mathematical thinking--the cognitive activity of doing mathematical research. By contrast, dealing with propositions such as "Every even number greater than 2 is the sum of two prime numbers," establishing the truth or falsity of which requires work--indeed, an unpredictable amount of work--would be seen as a deep challenge. Determining the truth or falsity of such propositions, by means of formal proof in the framework of an axiomatic system, would be the task facing a mathematical intelligence. Of course a successful proof, consisting of many lines, perhaps many pages, of text would be seen as a very complex cognitive structure, the fruit of an intelligent machine or mind.
Another domain that appealed greatly to many of the early movers of AI was chess. Once again, the primitive concepts of chess, such as "bishop," "diagonal move," "fork," "castling," and so forth were all seen as similar to mathematical definitions--essential to the game, of course, but posing little or no mental challenge. In chess, what was felt to matter was the development of grand strategies involving arbitrarily complex combinations of these definitional notions. Thus developing long and intricate series of moves, or playing entire games, was seen as the important goal.
As might be expected, many of the early AI researchers also enjoyed mathematical or logical puzzles that involved searching through clearly defined spaces for subtle sequences or combinations of actions, such as coin-weighing problems (given a balance, find the one fake coin among a set of twelve in just three weighings), the missionaries-and-cannibals puzzle (get three missionaries and three cannibals across a river in the minimum number of boat trips, under the constraint that there are never more cannibals than missionaries either on the boat, which can carry only three people, or on either side of the river), cryptarithmetic puzzles (find an arithmetically valid replacement for each letter by some digit in the equation "SEND+MORE=MONEY"), the Fifteen puzzle (return the fifteen sliding blocks in a four-by-four array having one movable hole to their original order), or even Rubik's Cube. All of these involve manipulation of hard-edged components, and the goal is to find complex sequences of actions that have certain hard-edged properties. By "hard-edged," I mean that there is no ambiguity about anything in such puzzles. There is no question about whether an individual is or is not a cannibal; there is no doubt about the location of a sliding block; and so forth. Nothing is blurry or vague.
These kinds of early preconceptions about the nature of the challenge of modeling intelligence on a machine gave a certain clear momentum to the entire discipline of AI--indeed, deeply influenced the course of research done all over the world for decades. Nowadays, however, the tide is slowly turning. Although some work in this logic-rooted tradition continues to be done, many if not most AI researchers have reached the conclusion--perhaps reluctantly--that the logic-based formal approach is a dead end.
What seems to be wrong with it? In a word, logic is brittle, in diametric opposition with the human mind, which is best described as "flexible" or "fluid" in its capabilities of dealing with completely new and unanticipated types of situations. The real world, unlike chess and some aspects of mathematics, is not hard-edged but ineradicably blurry. Logic and its many offshoots rely on humans to translate situations into some unambiguous formal notation before any processing by a machine can be done. Logic is not at all concerned with such activities as categorization or the recognition of patterns. And to many people's surprise, these activities have turned out to play a central role in intelligence.
It happens that as AI was growing up, a somewhat distinct discipline called "pattern recognition" (PR) was also being developed, mostly by different researchers. There was some but not much communication between the two disciplines. Researchers in PR were concerned with getting machines to do such things as read handwriting or typewritten text, visually recognize objects in photographs, and understand spoken language. In the attempts to get machines to do such things, the complexity of categories, in its full glory and in its full messiness, began slowly to emerge. Researchers were faced with questions like these: What is the essence of dog-ness or house-ness? What is the essence of 'A'-ness? What is the essence of a given person's face, that it will not be confused with other people's faces? What is in common among all the different ways that all different people, including native speakers and people with accents, pronounce "Hello"? How to convey these things to computers, which seem to be best at dealing with hard-edged categories--categories having crystal-clear, perfectly sharp boundaries?
These kinds of perceptual challenges, despite their formidable, bristling difficulties, were at one time viewed by most members of the AI community as a low-level obstacle to be overcome en route to intelligence--almost as a nuisance that they would have liked to, but couldn't quite, ignore. For example, the attitude of AI researchers would be, "Yes, it's damn hard to get a computer to perceive an actual, three-dimensional chessboard, with all of its roundish shapes, varying densities of shadows, and so forth, but what does that have to do with intelligence? Nothing! Intelligence is about finding brilliant chess moves, something that is done after the perceptual act is completely over and out of the way. It's a purely abstract thing. Conceptually, perception and reasoning are totally separable, and intelligence is only about the latter." In a similar way, the typical AI attitude about doing math would be that math skill is a completely perception-free activity without the slightest trace of blurriness--a pristine activity involving precise, rigid manipulations of the most crystalline of definitions, axioms, rules of inference--a mental activity that (supposedly) is totally isolated from, and totally unsullied by, "mere" perception.
These two trends--AI and PR--had almost no overlap. Each group pursued its own ends with almost no effect on the other group. Very occasionally, however, one could spot hints of another possible attitude, radically different from these two. The book Pattern Recognition, written in the late 1960s by Mikhail Bongard, a Russian researcher, seemed largely to be a prototypical treatise on pattern recognition, concerned mostly with recognition of objects and having little to do with higher mental functioning.2 But then in a splendid appendix, Bongard revealed his true colors by posing an escalating series of 100 pattern-recognition puzzles for humans and machines alike. Each puzzle involved twelve simple line drawings separated into two sets of six each, and the idea was to figure out what was the basis for the segregation. What was the criterion for separating the twelve into these two sets? Readers are invited to try the following Bongard problem, for instance.

Of course, for each puzzle there were, in a certain trivial sense, an infinite number of possible solutions. For instance, one could take the six pictures on the left of any given Bongard problem and say, "Category 1 contains exactly these six pictures (and no others) and Category 2 contains all other pictures." This would of course work in a very literal-minded, heavy-handed way, but it would not be how any human would ever think of it, except under the most artificial of circumstances. A psychologically realistic basis for segregation in a Bongard problem might be that all pictures in Category 1 would involve no curved lines, say, whereas all pictures in Category 2 would have at least one curved line. Or another typical segregation criterion would be that pictures in Category 1 would involve nesting (i.e., the presence of a shape containing another shape), and pictures in Category 2 would not. And so on. The following Bongard problems give a feeling for the kinds of issues that Bongard was concerned with in his work. Readers are challenged to try to find, for each of them, a very simple and appealing criterion that distinguishes Category 1 from Category 2.


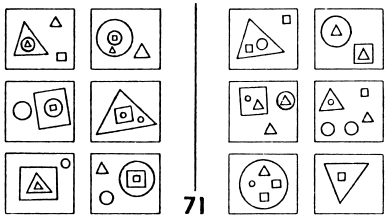

The key feature of Bongard problems is that they involve highly abstract conceptual properties, in strong contrast to the usual tacit assumption that the quintessence of visual perception is the activity of dividing a complex scene into its separate constituent objects followed by the activity of attaching standard labels to the now-separated objects (i.e., the identification of the component objects as members of various pre-established categories, such as "car," "dog," "house," "hammer," "airplane," etc.). In Bongard problems, by contrast, the quintessential activity is the discovery of some abstract connection that links all the various diagrams in one group of six, and that distinguishes them from all the diagrams in the other group of six. To do this, one has to bounce back and forth among diagrams, sometimes remaining within a single set of six, other times comparing diagrams across sets. But the essence of the activity is a complex interweaving of acts of abstraction and comparison, all of which involve guesswork rather than certainty.
By "guesswork," what I mean is that one has to take a chance that certain aspects of a given diagram matter, and that others are irrelevant. Perhaps shapes count, but not colors--or vice versa. Perhaps orientations count, but not sizes--or vice versa. Perhaps curvature or its lack counts, but not location inside the box--or vice versa. Perhaps numbers of objects but not their types matter--or vice versa. Somehow, people usually have a very good intuitive sense, given a Bongard problem, for which types of features will wind up mattering and which are mere distractors. Even when one's first hunch turns out wrong, it often takes but a minor "tweak" of it in order to find the proper aspects on which to focus. In other words, there is a subtle sense in which people are often "close to right" even when they are wrong. All of these kinds of high-level mental activities are what "seeing" the various diagrams in a Bongard problem--a pattern-recognition activity--involves.
When presented this way, visual perception takes on a very different light. Its core seems to be analogy-making--that is, the activity of abstracting out important features of complex situations (thus filtering out what one takes to be superficial aspects) and finding resemblances and differences between situations at that high level of description. Thus the "annoying obstacle" that AI researchers often took perception to be becomes, in this light, a highly abstract act--one might even say a highly abstract art--in which intuitive guesswork and subtle judgments play the starring roles.
It is clear that in the solution of Bongard problems, perception is pervaded by intelligence, and intelligence by perception; they intermingle in such a profound way that one could not hope to tease them apart. In fact, this phenomenon had already been recognized by some psychologists, and even celebrated in a rather catchy little slogan: "Cognition equals perception."
Sadly, Bongard's insights did not have much effect on either the AI world or the PR world, even though in some sense his puzzles provide a bridge between the two worlds, and suggest a deep interconnection. However, they certainly had a far-reaching effect on me, in that they pointed out that perception is far more than the recognition of members of already-established categories--it involves the spontaneous manufacture of new categories at arbitrary levels of abstraction. As I said earlier, this idea suggested in my mind a profound relationship between perception and analogy-making--indeed, it suggested that analogy-making is simply an abstract form of perception, and that the modeling of analogy-making on a computer ought to be based on models of perception.
A key event in my personal evolution as an AI researcher was a visit I made to Carnegie-Mellon University's Computer Science Department in 1976. While there, I had the good fortune to talk with some of the developers of the Hearsay II program, whose purpose was to be able to recognize spoken utterances. They had made an elegant movie to explain their work, which they showed me. The movie began by graphically conveying the immense difficulty of the task, and then in clear pictorial terms showed their strategy for dealing with the problem.
The basic idea was to take a raw speech signal--a waveform, in other words, which could be seen on a screen as a constantly changing oscilloscope trace--and to produce from it a hierarchy of "translations" on different levels of abstraction. The first level above the raw waveform would thus be a segmented waveform, consisting of an attempt to break the waveform up into a series of nonoverlapping segments, each of which would hopefully correspond to a single phoneme in the utterance. The next level above that would be a set of phonetic labels attached to each segment, which would serve as a bridge to the next level up, namely a phonemic hypothesis as to what phoneme had actually been uttered, such as "o" or "u" or "d" or "t." Above the phonemic level was the syllabic level, consisting, of course, in hypothesized syllables such as "min" or "pit" or "blag." Then there was the word level, which needs little explanation, and above that the phrase level (containing such hypothesized utterance-fragments as "when she went there" or "under the table"). One level higher was the sentence level, which was just below the uppermost level, which was called the pragmatic level.
At that level, the meaning of the hypothesized sentence was compared to the situation under discussion (Hearsay always interpreted what it heard in relation to a specific real-world context such as an ongoing chess game, not in a vacuum); if it made sense in the given context, it was accepted, whereas if it made no sense in the context, then some piece of the hypothesized sentence--its weakest piece, in fact, in a sense that I will describe below--was modified in such a way as to make the sentence fit the situation (assuming that such a simple fix was possible, of course). For example, if the program's best guess as to what it had heard was the sentence "There's a pen on the box" but in fact, in the situation under discussion there was a pen that was in a box rather than on it, and if furthermore the word "on" was the least certain word in the hypothesized sentence, then a switch to "There's a pen in the box" might have a high probability of being suggested. If, on the other hand, the word "on" was very clear and strong whereas the word "pen" was the least certain element in the sentence, then the sentence might be converted into "There's a pin on the box." Of course, that sentence would be suggested as an improvement over the original one only if it made sense within the context.
This idea of making changes according to expectations (i.e., long-term knowledge of how the world usually is, as well as the specifics of the current situation) was a very beautiful one, in my opinion, but it caused no end of complexity in the program's architecture. In particular, as soon as the program made a guess at a new sentence--such as converting "There's a pen on the box" into "There's a pen in the box"--it took the new word and tried to modify its underpinnings, such as its syllables, the phonemes below them, their phonetic labels, and possibly even the boundary lines of segments in the waveform, in an attempt to see if the revised sentence was in any way justifiable in terms of the sounds actually produced. If not, it would be rejected, no matter how strong was its appeal at the pragmatic level. And while all this work was going on, the program would simultaneously be working on new incoming waveforms and on other types of possible rehearings of the old sentence.
The preceding discussion implies that each aspect of the utterance at each level of abstraction was represented as a type of hypothesis, attached to which was a set of pieces of evidence supporting the given hypothesis. Thus attached to a proposed syllable such as "tik" were little structures indicating the degree of certainty of its component phonemes, and the probability of correctness of any words in which it figured. The fact that plausibility values or levels of confidence were attached to every hypothesis imbued the current best guess with an implicit "halo" of alternate interpretations, any one of which could step in if the best guess was found to be inappropriate.
I am sure that the figurative language I am using to describe Hearsay II would not have been that chosen by its developers, but I am trying to get across an image that it undeniably created in me, since that image then formed the nucleus of my own subsequent research projects in AI. Some other crucial features of the Hearsay II architecture that I have hinted at but cannot describe here in detail were its deep parallelism, in which processes of all sorts operated on many levels of abstraction at the same time, and its uniquely flexible manner of allowing a constant intermingling of bottom-up processing (i.e., the building-up of higher levels of abstraction on top of fairly solid lower-level hypotheses, much like the construction of a building) and top-down processing (i.e., the attempt to build plausible hypotheses close to the raw data in order to give a solid underpinning to hypotheses that make sense at abstract levels, something like constructing lower and lower floors after the top floors have been built and are sitting suspended in thin air).
Not too surprisingly, my first attempt to turn my personal vision of how Hearsay II operated into an AI project of my own was the sketching-out, in very broad strokes, of a hypothetical program to solve Bongard problems.3 However, the difficulties in actually implementing such a program completely on my own (this was before I had graduate students!) seemed so daunting that I backed away from doing so, and started exploring other domains that seemed more tractable. What I was always after was some kind of microdomain in which analogies at very high levels of abstraction could be made, yet which did not require an extreme amount of real-world knowledge.
Over the years, I developed a number of different computer projects, each one centered on a different microdomain, and thanks to the hard work of several superb graduate students, many of these abstract ideas were converted into genuine working computer programs. All of these projects are described in considerable detail in the book Fluid Concepts and Creative Analogies,4 co-authored by me and several of my students.
Here I would like to present in very quick terms one of those domains and the challenges that it involved, a project that clearly reveals how deeply Mikhail Bongard's ideas inspired me. The project's name is "Letter Spirit," and it is concerned with the visual forms of the letters of the roman alphabet. In particular, our goal is to build a computer program that can design all 26 lowercase letters, "a" through "z," in any number of artistically consistent styles. The task is made even more "micro" by restricting the letterforms to a grid. In particular, one is allowed to turn on any of the 56 short horizontal, vertical, and diagonal line segments--"quanta," as we call them--in the 2´6 array shown below. By so doing, one can render each of the 26 letters in some fashion; the idea is to make them all agree with each other stylistically.

To me, it is highly significant that Bongard chose to conclude his appendix of 100 pattern-recognition problems with a puzzle whose Category 1 consists of six highly diverse Cyrillic "A"s, and whose Category 2 consists of six equally diverse Cyrillic "B"s.

This choice of final problem is a symbolic message carrying the clear implication that, in Bongard's opinion, the recognition of letters constitutes a far deeper problem than any of his 99 earlier problems--and the more general conclusion that a necessary prerequisite to tackling real-world pattern recognition in its infinite complexity is the development of all the intricate and subtle analogy-making machinery required to solve his 100 problems and the myriad other ones that lie in their immediate "halo."
To show the fearsome complexity of the task of letter recognition, I offer the following display of uppercase "A"s, all designed by professional typeface designers and used in advertising and similar functions.

What kind of abstraction could lie behind this crazy diversity? (Indeed, I once even proposed that the toughest challenge facing AI workers is to answer the question: "What are the letters 'A' and 'I'?")
The Letter Spirit project attempts to study the conceptual enigma posed by the foregoing collection, but to do so within the framework of the grid shown above, and even to extend that enigma in certain ways. Thus, a Letter Spirit counterpart to the previous illustration would be the collection of grid-bound lowercase "a"s shown below, suggesting how intangible the essence of "a"-ness must be, even when the shapes are made solely by turning on or off very simple, completely fixed line segments.

I said above that the Letter Spirit project aims not just to study the enigma of the many "A"s, but to extend that enigma. By this I meant the following. The challenge of Letter Spirit is not merely the recognition or classification of a set of given letters, but the creation of new letterforms, and thereby the creation of new artistic styles. Thus the task for the program would be to take a given letter designed by a person--any one of the "a"s below, for instance--and to let that letter inspire the remaining 25 letters of the alphabet. Thus one might move down the line consecutively from "a" to "b" to "c," and so on. Of course, the seed letter need not be an "a," and even if it were an "a," the program would be very unlikely to proceed in strict alphabetical order (if one has created an "h," it is clearly more natural to try to design the "n" before tackling the design of "i"); but let us nonetheless imagine a strictly alphabetic design process stopped while under way, so that precisely the first seven letters of the alphabet have been designed, and the remaining nineteen remain to be done. Let us in fact imagine doing such a thing with seven quite different initial "a"s. We would thus have something like the 7´7 matrix shown below.

Implicit in this matrix (especially in the dot-dot-dots on the right side and at the bottom) are two very deep pattern-recognition problems. First is the "vertical problem"--namely, what do all the items in any given column have in common? This is essentially the question that Bongard was asking in the final puzzle of his appendix. The answer, in a single word, is: Letter. Of course, to say that one word is not to solve the problem, but it is a useful summary. The second problem is, of course, the "horizontal problem"--namely, what do all the items in any given row have in common? To this question, I prefer the single-word answer: Spirit. How can a human or a machine make the uniform artistic spirit lurking behind these seven shapes leap to the abstract category of "h," then leap from those eight shapes to the category "i," then leap to "j," and so on, all the way down the line to "z"?
And do not think that "z" is really the end of the line. After all, there remain all the uppercase letters, and then all the numerals, and then punctuation marks, and then mathematical symbols... But even this is not the end, for one can try to make the same spirit leap out of the roman alphabet and into such other writing systems as the Greek alphabet, the Russian alphabet, Hebrew, Japanese, Arabic, Chinese, and on and on. Of course, the making of such "transalphabetic leaps" (as I like to call them) goes way beyond the modest limits of the Letter Spirit project itself, but the suggestion serves as a reminder that, just as there are unimaginably many different spirits (i.e., artistic styles) in which to realize any given letter of the alphabet, there are also unimaginably many different "letters" (i.e., typographical categories) in which to realize any given stylistic spirit.
In metaphorical terms, one can talk about the alphabet and the "stylabet"--the set of all conceivable styles. Both of these "bets" are infinite rather than finite entities. The stylabet is very much like the alphabet in its subtlety and intangibility, but it resides at a considerably higher level of abstraction.
The one-word answers to the so-called vertical and horizontal questions--"letter" and "spirit"--gave rise to the project's name. There is of course a classic opposition in the legal domain between the concepts of "letter" and "spirit"--the contrast between "the letter of the law" and "the spirit of the law." The former is concrete and literal, the latter abstract and spiritual. And yet there is a continuum between them. A given law can be interpreted at many levels of abstraction. So too with the artistic design problems of the Letter Spirit project: there are many ways to extrapolate from a given seed letter to other alphabetic categories, some ways being rather simplistic and down-to-earth, others extremely sophisticated and high-flown. The Letter Spirit project does not by any means grow out of the dubious postulate that there is one unique "best" way to carry style consistently from one category to another; rather, it allows many possible notions of artistically valid style at many different levels of abstraction. Of course this means that the project is in complete opposition to any view of intelligence that sees the main purpose of mind as being an eternal quest after "right answers" and "truth." That the human mind can conduct such a quest, principally through such careful disciplines as mathematics, science, history, and so forth, is a tribute to its magnificent subtlety, but to do science and history is not how or why the mind evolved, and it deeply misrepresents the mind to cast its activities solely in the narrow and rigid terms of truth-seeking.
To convey something of the flavor of the Letter Spirit project, I offer the following sample style-extrapolation puzzle, which I hope will intrigue readers. Take the following gridbound way of realizing the letter "d" and attempt to make a letter "b" that exhibits the same spirit, or style.

One idea that springs instantly to mind for many people is simply to reflect the given shape, since one tends to think of "d" and "b" as being in some sense each other's mirror images. For many "d"s, this simple recipe for making a "b" might work, but in this case there is a somewhat troubling aspect to the proposal: the resultant shape has quite an "h"-ish look to it, enough perhaps to give a careful letter designer second thoughts.

What escape routes might be found, still respecting the rigid constraints of the grid?
One possible idea is that of reversing the direction of the two diagonal quanta at the bottom, to see if that action reduces the "h"-ishness.

To some people's eyes, including mine, this action slightly improves the ratio of "b"-ness to "h"-ness. Notice that this move also has the appealing feature of echoing the exact diagonals of the seed letter. This agreement could be taken as a particular type of stylistic consistency. Perhaps, then, this is a good enough "b," but perhaps not.
Another way one might try to entirely sidestep "h"-ishness would involve somehow shifting the opening from the bottom to the top of the bowl. Can you find a way to carry this out? Or are there yet other possibilities?
I must emphasize that this is not a puzzle with a clearly optimal answer; it is posed simply as an artistic challenge, to try to get across the nature of the Letter Spirit project. When you have made a "b" that satisfies you, can you proceed to other letters of the alphabet? Can you make an entire alphabet? How does your set of 26 letters, all inspired by the given seed letter, compare with someone else's?
The Letter Spirit project is doubtless the most ambitious project in the modeling of analogy-making and creativity so far undertaken in my research group, and as of this writing, it has by no means been fully realized as a computer program. It is currently somewhere between a sketch and a working program, and in perhaps a couple of years a preliminary version will exist. But it builds upon several already-realized programs, all of whose architectures were deeply inspired by the ideas of Mikhail Bongard and by principles derived from the architecture of the pioneering perceptual program Hearsay II.
To conclude, I would like to cite the words of someone whose fluid way of thinking I have always admired--the great mathematician Stanislaw Ulam. As Heinz Pagels reports in his book The Dreams of Reason, one time Ulam and his mathematician friend Gian-Carlo Rota were having a lively debate about artificial intelligence, a discipline whose approach Ulam thought was simplistic. Convinced that perception is the key to intelligence, Ulam was trying to explain the subtlety of human perception by showing how subjective it is, how influenced by context. He said to Rota, "When you perceive intelligently, you always perceive a function, never an object in the physical sense. Cameras always register objects, but human perception is always the perception of functional roles. The two processes could not be more different.... Your friends in AI are now beginning to trumpet the role of contexts, but they are not practicing their lesson. They still want to build machines that see by imitating cameras, perhaps with some feedback thrown in. Such an approach is bound to fail..."
Rota, clearly much more sympathetic than Ulam to the old-fashioned view of AI, interjected, "But if what you say is right, what becomes of objectivity, an idea formalized by mathematical logic and the theory of sets?"
Ulam parried, "What makes you so sure that mathematical logic corresponds to the way we think? Logic formalizes only a very few of the processes by which we actually think. The time has come to enrich formal logic by adding to it some other fundamental notions. What is it that you see when you see? You see an object as a key, a man in a car as a passenger, some sheets of paper as a book. It is the word 'as' that must be mathematically formalized.... Until you do that, you will not get very far with your AI problem."
To Rota's expression of fear that the challenge of formalizing the process of seeing a given thing as another thing was impossibly difficult, Ulam said, "Do not lose your faith--a mighty fortress is our mathematics," a droll but ingenious reply in which Ulam practices what he is preaching by seeing mathematics itself as a fortress!
If anyone else but Stanislaw Ulam had made the claim that the key to understanding intelligence is the mathematical formalization of the ability to "see as," I would have objected strenuously. But knowing how broad and fluid Ulam's conception of mathematics was, I think he would have been able to see the Letter Spirit architecture and its predecessor projects as mathematical formalizations.
In any case, when I look at Ulam's key word "as," I see it as an acronym for "Abstract Seeing" or perhaps "Analogical Seeing." In this light, Ulam's suggestion can be restated in the form of a dictum--"Strive always to see all of AI as AS"--a rather pithy and provocative slogan to which I fully subscribe.
1 For more on this, see "Waking Up from the Boolean Dream," Chapter 26 of my book, Metamagical Themas (New York: Basic, 1985).
2 See Mikhail Moiseevich Bongard, Pattern Recognition (New York: Spartan Books, 1970).
3 See Chapter 19 of my book Gödel, Escher, Bach (New York: Basic, 1979) for this sketched architecture.
4 Douglas R. Hofstadter and the Fluid Analogies Research Group, Fluid Concepts and Creative Analogies: Computer Models of the Fundamental Mechanism of Thought (New York: Basic, 1995).