
The Mentor Section
This one is quite different from the Solver section: there is no problem-solving task here.The user is expected to play the role of Phaeaco's mentor, attempting to teach visual patterns to Phaeaco by presenting (drawing) those patterns, optionally pairing them with a linguistic description. Alternatively, the mentor may test Phaeaco's knowledge by presenting a pattern and expecting Phaeaco to provide the (learned) linguistic description. The reverse (providing the linguistic description and expecting Phaeaco to draw a corresponding visual pattern) has not been implemented yet, but it is included in the possibilities for the future.
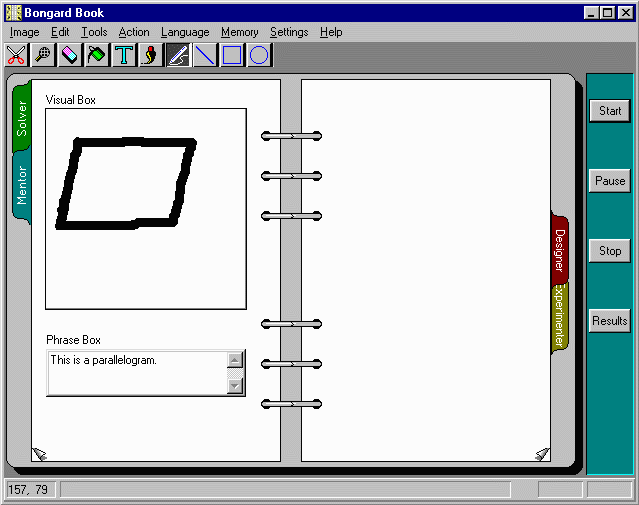
As an example, a parallelogram has been "hand-drawn" in the visual area (with the "pencil"-tool which is highlighted on the toolbar), while the phrase "This is a parallelogram." has been entered in the phrase-box. It should be understood that the visual area is a black-and-white square matrix (200 x 200), while the phrase-box is a regular editing area where characters can be typed. After entering the visual and linguistic input, the mentor clicks on the "Start" button (in the dark cyan area on the right), and allows the program to perform visual and linguistic analysis of the input (please click on it to get an idea about at least the results of visual analysis).
What happens during the visual analysis
During this phase (which is performed prior to the linguistic analysis) Phaeaco starts by detecting the lowest-level features of the image, continuing to higher level ones as soon as possible. Among the lowest features that can be detected are pieces of straight lines. In particular, Phaeaco is interested in locating first the "median" (middle) parts of linear pieces of the input. For example, the parallelogram shown above consists of four not-very-straight and rather thick sides. The program first discovers that each of these four pieces is rather long, so it is not interested in the actual width or the "border pixels" of each piece (pixels where the black area borders with white). Rather, it is concerned with "median" pixels. After locating a few median pixels on each piece, it observes that they can be approximated with a straight line, and so it creates such a line, which is an abstraction of the thick, hand-drawn real line. The result of this work can be seen on this page, where the abstracted straight lines have been superimposed with yellow color over the actual image of the parallelogram. Also shown on that page are the intersection points of the four sides.
While identifying several of these features, Phaeaco builds an internal representation out of those features. For example, the parallelogram may be found to consist of four lines, four meeting points (of those four lines), two pairs of parallel lines, two horizontal lines, two pairs of lines with equal lengths, two pairs of equal angles, and possibly even more. The internal representation is not a simple list of the above features, but a rather intricate network of connected nodes, with each node representing a feature, or a relation among features. The exact details of the representation are too many and complex to be explained on this web page. Suffice it to say that the architecture follows the general cognitive guidelines proposed by D. R. Hofstadter in the early '80s, and best explained as an architectural paradigm in his book: "Fluid Concepts and Creative Analogies".
The search for visual features is not exhaustive, but probabilistic. This means that Phaeaco may initially "see" a slightly different set of features given the same input, depending on the run. In general, however, given enough time, it will eventually converge to more-or-less the same set of features (the same representation). It should be noted that the statement "given enough time" does not refer to eternity: the above parallelogram, given an average computer of the end of the second millennium (e.g., a Pentium PC at 1.0 GHz), is fully perceived within around 1/2 second. Thus, for the representation to remain incomplete, the visual analysis time must be restricted to the millisecond range.
The whole representational network is stored in short-term memory (STM) and is accessible through a single node, which represents "what the program just saw" (the parallelogram, in our example). The representation does not remain in STM indefinitely: the linkages of the network fade as time goes by, thus making it progressively harder to reach all details. If a similar input is given in the near future, the representation is reinforced, and its linkages become more resistant to fading. Eventually, after a small number of repetitions (depending on how complex the input is) most of the linkages between nodes become sufficiently strong for the representation to be copied to the long-term memory (LTM). Once in LTM, the representation can be retrieved any time in the future, including a different run of the program, because the LTM is saved on disk at program exit, and restored at program start. Time is not implemented through real time (as measured by the computer's clock), but by simulated time, which advances according to the number of visual inputs. This is a mere convenience for the program's mentor, else the latter would need to refresh the program's memory regularly, in real time, lest the program should become amnesic after a no-training period.
Apparently, there is a myriad of representational details which cannot be described on this web page. The author will provide a reference as soon as a publication becomes available.
The Solver Section
By clicking on the dark green tag labeled "Solver" we move to Phaeaco's Solver section.
The Designer Section
The brown tag of the notebook labeled "Designer" turns to Phaeaco's Designer section. This section is not implemented yet. It is a provision for the future, when the program will be able to design Bongard problems of its own.
Last update: 04/14/00