This text is an informal critique of the choice of representation of input in RF4 (Saito and Nakano, 1993), pertaining to Bongard problems, the author's domain of research. I give the main subject following a general introduction.
RF4 is "a concept learning algorithm" presented in a 1993 paper (see link, above), which "adaptively improves its concept learning efficiency." RF4 works in a space of first-order logic formulas, which it searches performing "a depth-first search on the basis of five criteria for pruning undesirable formulae and five transformation rules for combining formulae" (from the abstract of the paper above). I am not concerned here with the particular details of RF4, not even with its merits, which might be important in certain areas of computer science and artificial intelligence. What concerns me is the choice of Bongard problems by Saito and Nakano, as a domain which exemplifies the virtues of RF4. In particular, S&N claim that RF4, as implemented on a personal computer in C, "solved 41 out of 100 Bongard problems within a few seconds for each problem." This claim, by itself, is hardly interesting. After all, there is the trivial "algorithm", which, when presented with any Bongard problem (henceforth, BP) "solves" it in a matter of a few nanoseconds, depending on the computer used: it is a 2x100 table, the first column of which contains the incremental number of the BP, while the second column contains the corresponding solution, in plain English. You enter the BP-number in this "program", and -- voila! you get the solution. What more could we expect from an automation of intelligence?
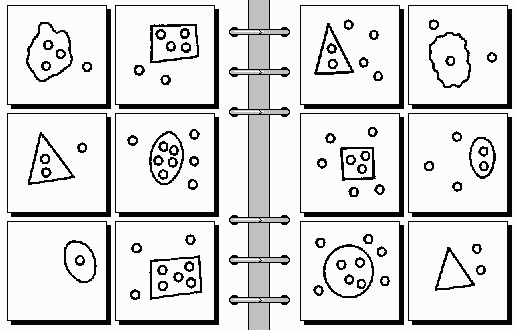
RF4, of course, does not work that way. In RF4, BP's are given not as incremental numbers of a table, but as first-order logic formulas. For example, the first box on the left side of BP #6 (a single outlined triangle) might be given by something like:
polygon(X) & outlined(X) & angles(X) = 3
I say "might be given" as above because, unfortunately, S&N never give us a complete example of input representation in their 1993 paper. I had to make an educated guess for the above formula from the solution to BP #6, which they do give:
forall B in boxes, forall X in B, angles(X) = 3 --> class1
So, in RF4, the input "BP #6" (for example) is not given as "location 6 of the 2x100 table", as in our trivial algorithm above, but as a collection of 12 formulas (6 for the left and 6 for the right side) similar to the first one, above.
Cases like BP #6 are misleading, because of their simplicity. When we see a single outlined triangle in a box it is difficult to think that a description like "polygon(X) & outlined(X) & angles(X) = 3" does not describe accurately what we see in the box. In this particular problem it happens that it does, because nothing else is relevant in its solution. Suppose we do not know the solution beforehand, however (which is the natural thing to expect for BP's). Why would not the location -- in coordinates -- of the triangle be specified? After all, we might be dealing with BP #8, where the solution has to do precisely with the absolute locations of the outlined areas within their boxes. Why would not the size of the triangle be relevant? (Actually, the length of each of its sides.) Problem #2 has to do with size. And the slope of each of its sides? How about the quality of the sides, which is "plain straight line", as opposed to the qualities of lines in BP #9 and BP #107? And how about the line-thickness, which seems to be around 2 pixels (depending on resolution)?
We thus see that, even in cases of simple triangles, the specification in terms of a first-order logic formula has to be quite long, if we want to be honest and not exclude a priori some feature, an exclusion which would certainly guide the program towards the solution, if the latter does not contain such a feature. Else, if we include only the relevant features in the input-description, we clearly perform an act of cheating. The degree of cheating is inversely proportional to the length of the first-order formula. For example, the formula "polygon(X) & outlined(X) & angles(X) = 3" cheats to a certain degree because it contains only three predicates, excluding most of the others mentioned in the previous paragraph; the formula "outlined(X) & angles(X) = 3" cheats more; the formula "angles(X) = 3", even more; finally, the "formula" "6th problem, 1st box -- now tell me the solution" (taken from our earlier 2x100 table-example) cheats as much as it is possible.
Yet, all the above discussion presupposes that we know what the possible features are, in order to include them in the (long) formula. Even this, however, is not always possible. Consider, for example, BP #29 (actually shown in S&N's paper):

What could the description of the top-left-most box on the left side be? How do we specify an irregular curve through a first-order formula? Could it be that we do not need to be very precise about its exact shape, describing it simply as a "closed curve"? But how do we know a priori whether its shape is irrelevant, without knowing the solution? In this particular problem (#29) it happens that the shape is irrelevant. But look now at BP #20:
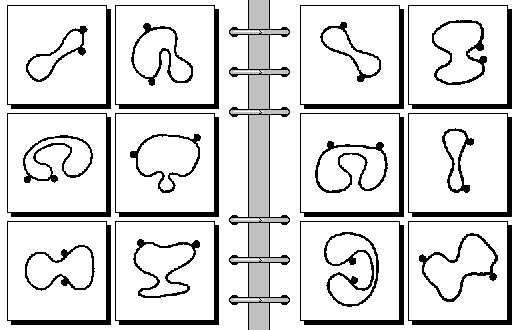
Is shape still irrelevant? Would it be honest to specify something like "closed_curve(X) & bulges(X) = 2 &..." for the first box (top-left, left side)? But the whole point in this problem is to realize precisely that there are two bulges on each curve. Once that is done, finding out about the placement of the two dots in relation to the two bulges is trivial. So if we want to be honest, we should avoid using predicates like "bulges(X)", and let the program discover those bulges... but from what? Predicates like "closed_curve(X)" do not seem to be very helpful. Should not the specification of the curve be given in terms of a very long sequence of short straight lines, each meeting its previous and next line at its two ends? This seems to be a fully honest approach, if all the coordinates, lengths, and slopes of the lines in this sequence are given. But are we serious? How on earth do we do this with a first-order formula?! How long does this formula have to be, and how can it be manipulated to infer the existence of the two "bulges" from it?
The conclusion that I draw from the previous paragraphs is that first-order formulas are the wrong kind of representation regarding Bongard problems. If they are short enough to be manageable, the representation is cheating; and if they are long enough to be honest, the representation is unmanageable. Consequently, raw (unprocessed) bit-maps, with black and white pixels are superior as input specifications, because everything that there is to be discovered about the contents of the box is there, in front of the program's eye, waiting to be discovered by the program's mind, un-preprocessed by human helpers.
This last observation apparently generalizes beyond Bongard problems, applying equally to other domains in cognitive science. Whenever the input in a cognitive domain is complex, its initial specification should avoid all manual (human-guided) preprocessing and pruning, allowing the automated system to arrive by itself at any pithy, concise description which possibly exists. Raw, unordered information comes first; the crystallized, highly ordered re-description of it comes much later, after laborious processing. Most of the initial efforts in 20th century artificial intelligence ("GOFAI") had this principle backwards: they would start the automated processing from the crystallized form, facing the insurmountable difficulties of the lost raw information only later, in the form of non-scalability, and impracticability. RF4 is nothing but a genuine product of that age and philosophy in artificial intelligence.
A related link on the web is Alexandre Linhares's critique of RF4 (in PDF format).
Last update: 09/14/03